La curiosità del mese a cura di Daniele Spiga

Avete mai disegnato una mappa in scala del Sistema Solare? A dirlo, sembra un banale esercizio: provateci, facendo stare tutto su un foglio di comune formato A4, e quando dovrete segnare i pianeti vedrete che non vi basterà la più fine delle punte di matita per segnarli con le loro corrette dimensioni in proporzione alle loro distanze.
La verità è che la nostra intuizione non si capacita proprio di quanto sia realmente grande lo spazio tra i corpi orbitanti intorno al Sole. Ma soprattutto… sbagliamo a immaginarci lo spazio tra le orbite planetarie come totalmente vuoto.
Se c’è qualcosa che è risultato evidente dagli anni ’80 a oggi, è proprio che là fuori ci sono svariate centinaia di migliaia di asteroidi di cui la maggior parte orbita più o meno stabilmente tra Marte e Giove, mentre molte altre decine di migliaia di essi attraversano regolarmente l’orbita della Terra e dei pianeti interni, e infine alcune migliaia di essi (i famosi PHA, Potentially Hazardous Asteroids) di quando in quando passano molto vicini alla Terra, perciò vanno tenuti attentamente d’occhio.
Alcuni di essi orbitano su orbite più piccole di quella terrestre, e fanno un giro intorno al Sole in un tempo inferiore ad un anno. Altri orbitano su orbite più grandi, e ci mettono più di un anno a completare un giro. Ma alcuni di essi, per puro caso, fanno un giro intorno al Sole in quasi un anno esatto, quasi come la nostra Terra, ed è di questi strani tipi che ci occupiamo oggi.
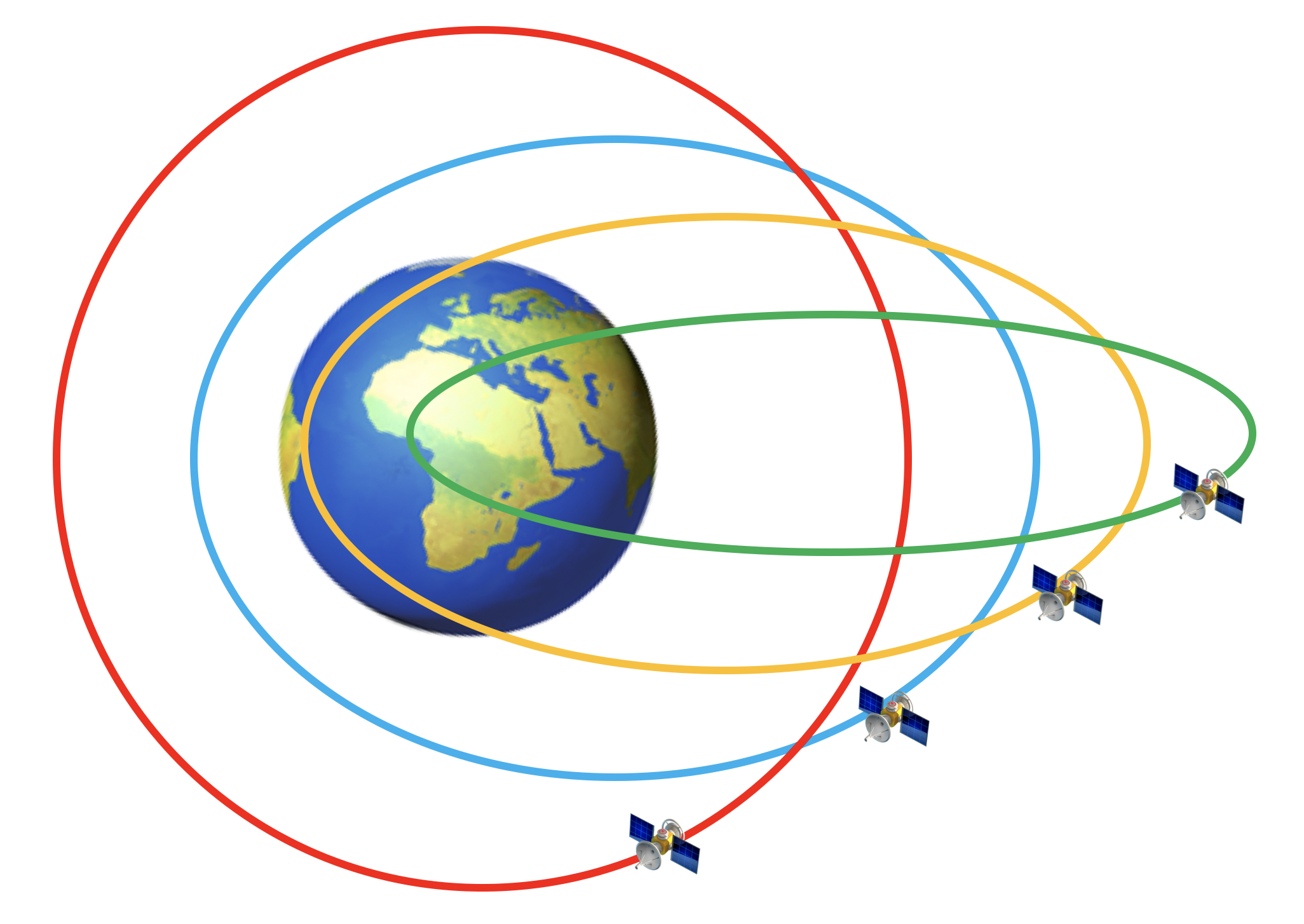
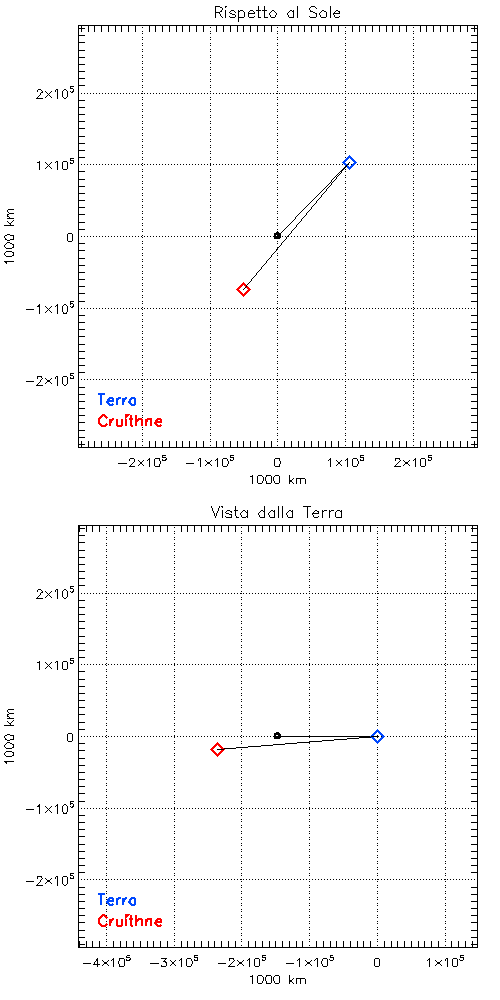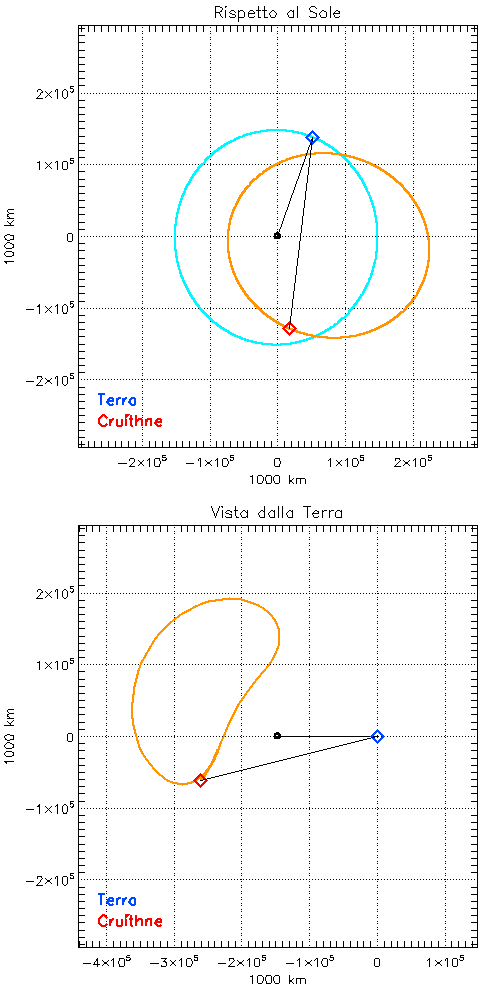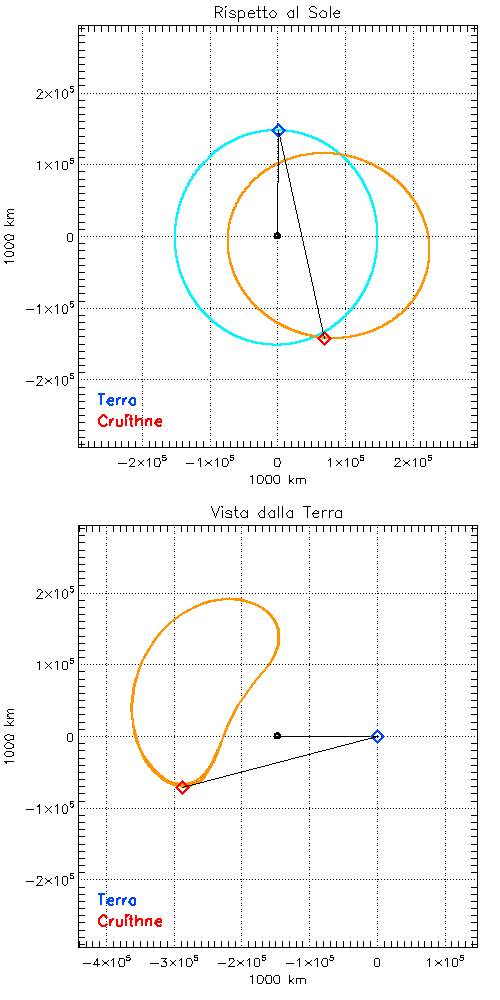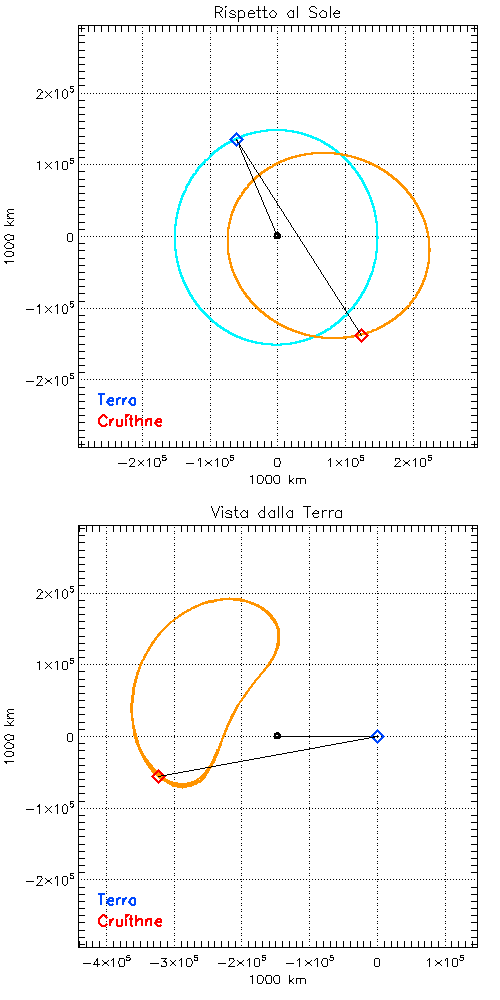
Ad esempio, consideriamo 3753 Cruithne: un asteroide di 5 km di diametro con un periodo orbitale di 364 giorni, giusto uno in meno di quello della Terra (Figura 1).
Dalla terza legge di Keplero deduciamo che l’orbita di Cruithne e della Terra hanno quasi esattamente lo stesso semiasse maggiore, però l’orbita di Cruithne è molto più eccentrica. Quindi, le due orbite non coincidono ma, siccome l’eccentricità dell’orbita non ha nessunissimo effetto sul periodo orbitale (Figura 2), sono percorse nello stesso tempo (o, come si dice più esattamente, in risonanza orbitale 1:1).
Ora, supponiamo che Cruithne e la Terra si trovino vicine fra loro proprio in questo momento; al passare del tempo, i due oggetti si separeranno, ma fra un anno si ritroveranno a essere all’incirca nelle stesse posizioni. Il risultato è che Cruithne, dal nostro punto di vista, sembrerà avere descritto un’orbita intorno alla Terra!
Questo è il motivo per cui asteroidi in risonanza orbitale 1:1 vengono anche definiti “quasi-satelliti” e Cruithne, con un certo abuso di linguaggio, è anche chiamato “la seconda luna della Terra”. In realtà, Cruithne rimane sempre fuori dalla sfera di Hill della Terra e quindi non è una nostra luna. Però la composizione dei due moti, ellittico quello di Cruithne e quasi-circolare quello della Terra, conferisce alla traiettoria di Cruithne, sempre vista dalla Terra, una caratteristica forma a “fagiolo” (Figura 3).
Cruithne non è l’unico quasi-satellite della Terra: ve ne sono altri, come 2002 AA29 e 2003 YN107, tutti caratterizzati da orbite come quella descritta. Rientra in questa categoria anche 469219 Kamo’oaleva, un asteroide di circa 100 metri originatosi dalla nostra Luna e ora diventato quasi-satellite della Terra. Eppure, sarebbe arrogante da parte nostra pensare di averne l’esclusiva nel sistema solare: si conoscono quasi-satelliti (per la verità instabili) di Venere, Nettuno, e potrebbero tranquillamente essercene anche di Marte, Giove, Saturno, e Urano.
E soprattutto, esistono quasi-satelliti anche di altri satelliti: se due satelliti orbitano intorno a un pianeta con lo stesso periodo orbitale, allora ciascuno di essi vede l’altro girargli intorno nello stesso tempo. Di quest’ultimo tipo, conosciamo un solo esempio: quello formato da Giano ed Epimeteo (Figura 4), due satelliti di Saturno, che si trovano praticamente sulla stessa orbita poco fuori dai suoi anelli, con un periodo di 16 ore e mezza circa.
A questo punto, qualcuno potrebbe fare un’osservazione più che appropriata: visto che un quasi-satellite della Terra si avvicina periodicamente ad essa, e visto che tra di esso e la Terra si esercita un’attrazione gravitazionale, ogni volta Cruithne dovrebbe avvicinarsi un po’ alla Terra e alla fine… dovrebbe caderci addosso (e viste le sue dimensioni, causerebbe un’estinzione di massa…)!
E’ il caso che facciamo tutti testamento?
No, ancora no…!
Ci sono vari PHA là fuori, ma i quasi-satelliti non sono fra questi. Anzi, proprio il contrario: esiste un interessante giochino di meccanica celeste, assolutamente controintuitivo, che protegge i quasi-satelliti dalle collisioni. E per capirlo, conviene considerare proprio il sistema Giano-Epimeteo.
Il meccanismo, per sommi capi, funziona così (mostrato in Figura 5, fortemente amplificato per renderlo più visibile): attualmente, Epimeteo, che è il meno massiccio dei due, orbita a una distanza da Saturno appena 50 km più piccola di quella di Giano. Dunque, la terza legge di Keplero ci insegna che si muove più velocemente di Giano e per questo completa un giro in un tempo leggermente inferiore, tendendo a raggiungerlo alle spalle.
Quando gli arriva abbastanza vicino, inizia a sentire la gravità di Giano e viene effettivamente attratto verso di esso, ma… non avviene quello che ci aspetteremmo, cioè un “tamponamento” spaziale.
Infatti, se si imprime una spinta ad un corpo orbitante, il risultato non è lo stesso che otterremmo dando una spinta ad una giostra: al contrario, l’aumento di velocità causa una maggiore forza centrifuga che spinge Epimeteo verso l’esterno col risultato di… aumentarne leggermente la distanza da Saturno.
Ma allora anche il periodo orbitale aumenta, ed aumenta in misura maggiore del raggio dell’orbita, perciò… paradossalmente, spingendo un corpo ad accelerare lungo la sua orbita, lo rallentiamo! Come risultato, Epimeteo si sposta su un’orbita più lenta di quella di Giano, e ora è quest’ultimo a muoversi più veloce… quindi inizia a distaccarlo!
Ma, dopo circa 4 anni, i ruoli si scambiano: ora Giano va più veloce e, mentre Epimeteo sente il suo fiato sul collo… la gravità di Giano lo “frena” spostandolo su un’orbita di raggio più piccolo, ma su cui viaggia più veloce, e come risultato Epimeteo inizierà a fuggire in avanti fino a quasi raggiungere Giano da dietro, e così via, in un ciclo che dura circa 8 anni, con un continuo scambio di energia e momento angolare.
La cosa interessante è che, pur condividendo la stessa orbita, i due corpi non solo non si affiancano mai e non si sorpassano mai, ma nemmeno si avvicinano a meno di 10000 km.
Un comportamento esemplare, che dovrebbe essere imitato da molti automobilisti, non credete?
Tuttavia, un aspetto più curioso è che l’orbita di Epimeteo, dal punto di vista di Giano, assume la forma di una specie di C; per questo, orbite di questo tipo si dicono a “ferro di cavallo” e sono proprio caratteristiche dei quasi-satelliti tramite il meccanismo descritto.
Infatti, anche la nostra Cruithne descrive, sempre dal punto di vista della Terra, un’orbita di questo tipo, anche se su tempi molto più lunghi: con un periodo di 770 anni.
In questo momento, per esempio, Cruithne ci precede di circa 70 gradi e – in media – si sta allontanando dalla Terra.
Anche in questo caso, i due corpi non si affiancano, non si sorpassano, e non si avvicinano a meno di 12 milioni di km; una distanza di sicurezza assolutamente irreprensibile per il codice della strada spaziale.
Rispetto a Giano e Epimeteo, però, la cosa è resa più complicata dall’eccentricità dell’orbita di Cruithne, per cui è tutto il “fagiolo” che si sposta periodicamente (Figura 6) lungo il ferro di cavallo. Ma non è finita!
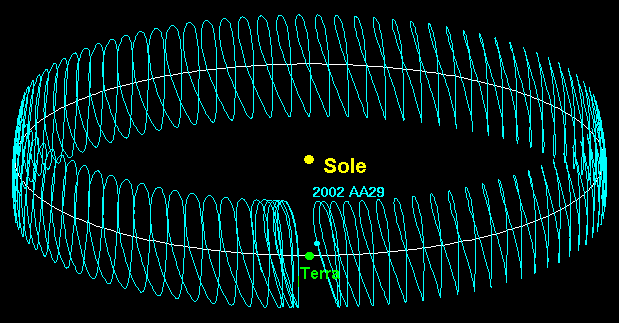
L’orbita di Cruithne è inclinata rispetto alla nostra, quindi… la sua traiettoria appare dalla Terra come un’elegante spirale, con il suo asse che descrive l’orbita a ferro di cavallo, simile a quella di 2002 AA29 mostrata in Figura 7.
E ora, che abbiamo imparato (a prezzo di un bel mal di testa…) di quali acrobazie è capace la gravità, continuiamo forse a vedere il nostro Sistema Solare come un meccanismo ordinato, regolare, prevedibile e un po’ noioso, di cui ormai abbiamo capito proprio tutto-tutto-tutto? No, vero?
Ma aspettate un po’… che svilupperemo il tema delle risonanze orbitali … e ci dovremo ricredere un’altra volta!