Astrocuriosità | giugno 2025 – Raggi X allo specchio: II puntata – L’indice di rifrazione più pazzo del mondo

La curiosità del mese a cura di Daniele Spiga

Immagine di Daniele Spiga

Prosegue la serie introduttiva all’ottica dei raggi X, parte del progetto AOX (P.I. Marta Civitani, INAF-Brera) finanziato da ASI per lo sviluppo di ottiche monolitiche per raggi X in vetro sottile.

Bene: facciamo un bel respiro… e soffermiamoci un momento sull’interazione dei raggi X con la materia, cosa che cercheremo di fare senza formule e matematica (che è un po’ come cercare di ricostruire la storia dell’antico Egitto senza conoscere i geroglifici, ma ci proviamo lo stesso). Nella puntata precedente, dedicata al fenomeno della riflessione totale che rende possibile realizzare specchi per telescopi a raggi X, avevamo visto che questa dipendeva dal fatto che l’indice di rifrazione di tutti i materiali nei raggi X fosse minore di 1, pur discostandosene di pochissimo. E avevamo lasciato in sospeso due “piccole” domande:

  1. perché questo indice di rifrazione, che – lo abbiamo capito, ormai – dipende dalla frequenza, e che normalmente è maggiore di 1, nei raggi X decide di essere minore di 1? Cosa c’è di particolare nella materia che fornisce questo “privilegio” [1] ai raggi X?
  2. visto che l’indice di rifrazione n è il rapporto tra la velocità della luce nel vuoto c e la velocità della luce nel mezzo v, il fatto che n < 1 comporta v > c, e cioè che i raggi X viaggino in un mezzo materiale più veloce di quanto non facciano nel vuoto. Ma… questo dovrebbe essere vietato dalla teoria della relatività! Come la mettiamo?

Iniziamo dalla prima domanda, cercando di rappresentare quello che accade quando un’onda elettromagnetica attraversa la materia, e cerchiamo in particolare di capire perché deve modificare la propria velocità.

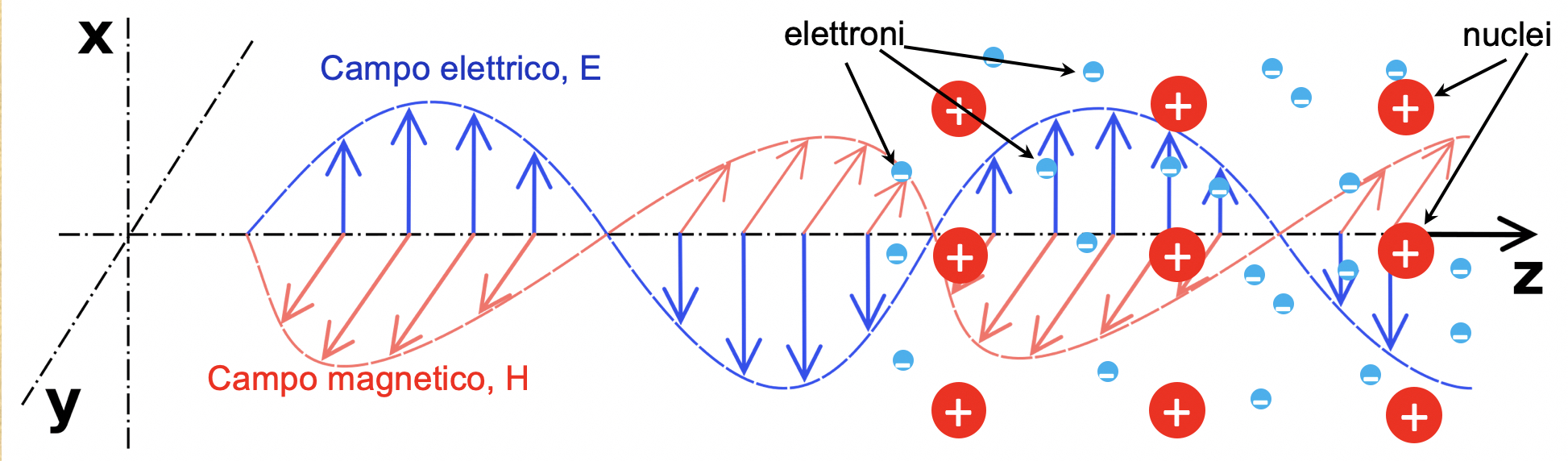
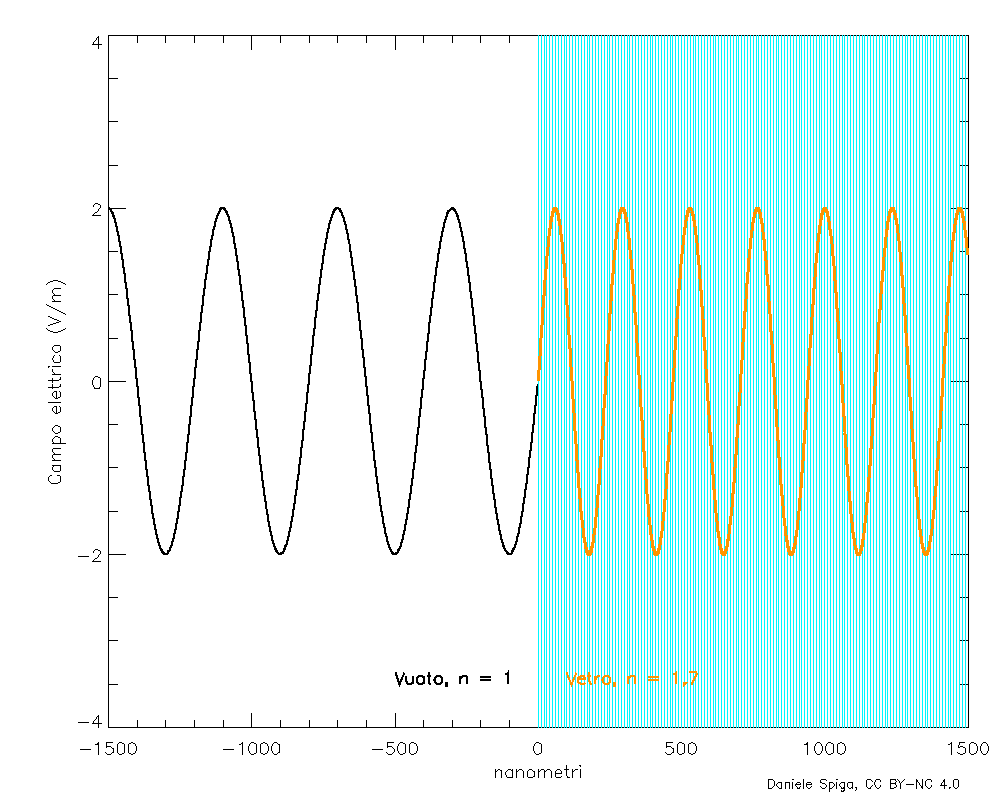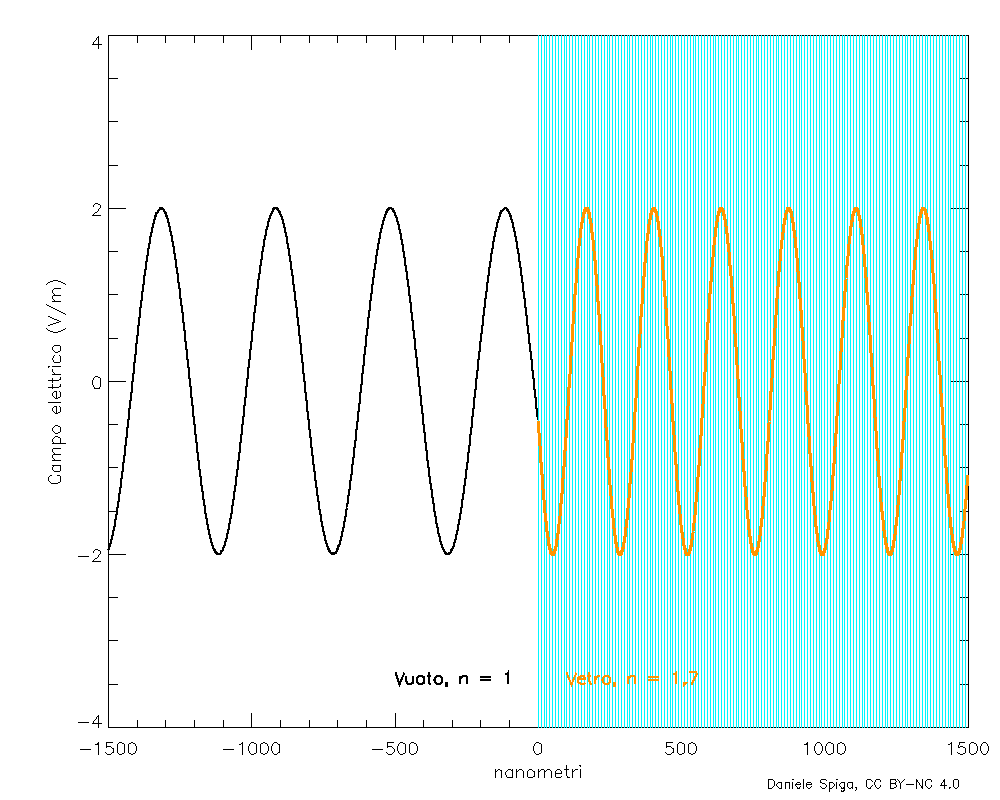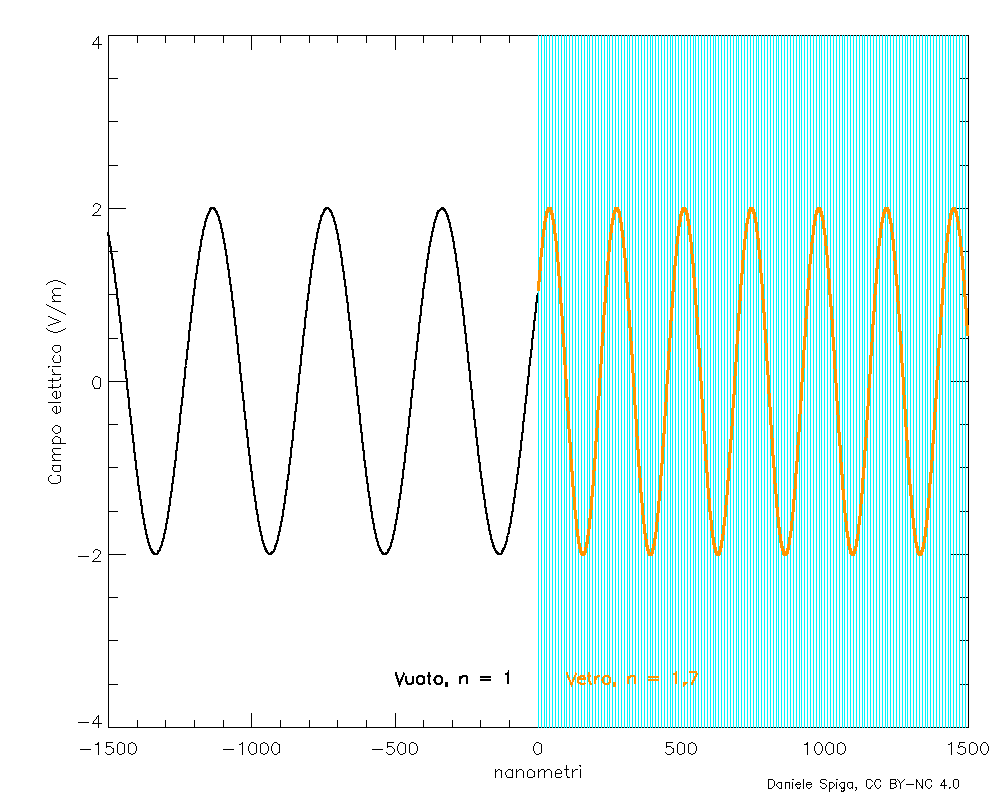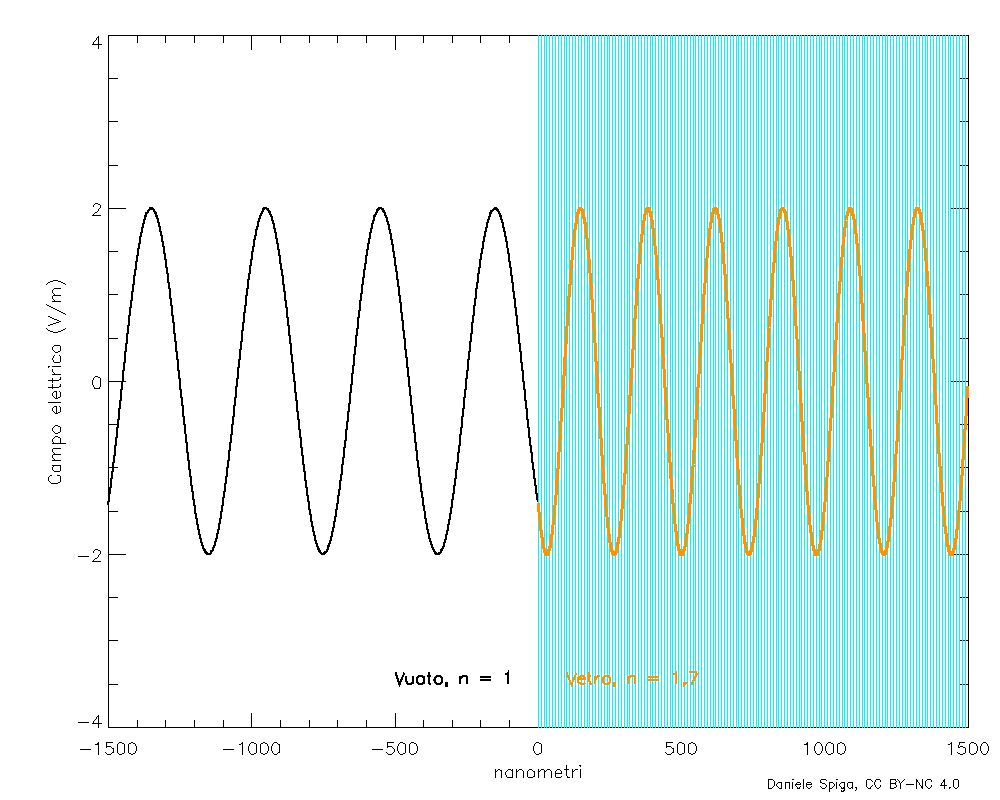
            Le onde elettromagnetiche sono oscillazioni di campi elettrici e magnetici che si sostengono a vicenda, mentre si propagano attraverso lo spazio e il tempo. Consideriamo dapprima il tipo più semplice possibile di onda, composta da una sola frequenza: questo tipo di onda, perfettamente periodica e infinitamente estesa (Figura 2), è detta sinusoidale (per via del suo profilo) o monocromatica (perché, nella luce visibile, una singola frequenza corrisponde a un solo colore, Figura 3). Definire la sua velocità non è immediato come lo sarebbe definire la velocità di una palla, in quanto un’onda non ha una posizione definita nello spazio. Però, un’onda presenta pur sempre delle creste: se seguiamo lo spostamento di una qualunque di esse nel tempo (Figura 4), possiamo misurare facilmente la loro velocità. Oppure, potremmo misurare la velocità con cui si spostano le “valli” dell’onda, oppure i punti a metà fra le valli e le creste… ma otterremo sempre lo stesso numero vF: quella che si chiama velocità di fase di un’onda, così denominata perché indica la velocità con cui si sposta un punto con una certa fase (ovvero su una cresta, o in una valle, o in un qualunque punto fra esse). L’indice di rifrazione è appunto il rapporto n = c/vF.

Ora, i campi elettromagnetici agiscono sulle cariche elettriche, e la materia è composta appunto di particelle dotate di carica elettrica, che iniziano ad oscillare quando un’onda elettromagnetica le attraversa (Figura 2), non diversamente da un insieme di barchette che oscillano al passare di un’onda nel mare in cui galleggiano. Qui però dobbiamo distinguere tra due tipi principali di particelle che compongono la materia: ci sono gli elettroni, di carica negativa e leggerissimi (pertanto, estremamente mobili), e i nuclei atomici, di carica positiva e molto più massicci, che pertanto possiamo assumere immobili a causa della loro inerzia. Possiamo quindi comprendere, almeno intuitivamente, che al passaggio di un’onda elettromagnetica (la chiameremo d’ora in poi onda incidente) gli elettroni inizieranno ad oscillare vivacemente alla stessa frequenza, mentre i nuclei non faranno una piega o quasi. Sono proprio queste oscillazioni degli elettroni che causano il cambiamento della velocità dell’onda. E per capire quello che succede, consideriamo dapprima il caso della rifrazione a cui siamo abituati, quella che rallenta la luce (Figura 4), ovvero n > 1. Quando una carica elettrica viene fatta oscillare, inizia a irraggiare onde elettromagnetiche alla stessa frequenza, proprio come una piccola antenna. Gli elettroni sono piccolini, perciò ciascuno di essi irradia una piccola quantità di radiazione, ma in compenso sono tanti: un cm3 di vetro, per darvi un’idea, ne contiene circa 1024 (un milione di miliardi di miliardi). E tutti questi elettroni irraggiano, come tanti piccoli coristi che emettono la stessa frequenza intonata dal direttore del coro e per di più, tutti ben sincronizzati fra loro e con l‘onda incidente o come si dice, tutti in fase. E …cosa succede quando tante sorgenti emettono radiazione tutte sincronizzate in fase? Interferiscono, cancellandosi in alcuni punti e rafforzandosi in altri. Ma allora, qual è il risultato dell’interferenza di queste ondine, prima fra di esse, e poi con l’onda incidente?

Qui le cose richiederebbero un po’ di calcoli,[2] ma il risultato è che l’interferenza di tutte le onde emesse dagli elettroni oscillanti si propaga 1) nella stessa direzione dell’onda incidente (e in quella opposta, ma per ora questa non ci interessa), 2) a velocità c come l’onda incidente, 3) alla stessa frequenza f dell’onda incidente ma 4) in ritardo di ¼ di periodo rispetto all’onda incidente. Pertanto, ogni strato di materiale rifrangente (acqua, vetro, ecc.) che viene attraversato dall’onda incidente genera una piccola onda, che, sovrapponendosi all’onda incidente stessa, ne ritarda la fase di una piccola quantità (Figura 5). Ma, siccome la frequenza è rimasta la stessa, il ritardo della fase può solo risultare in una diminuzione della velocità di fase dell’onda risultante.

Sembra semplice, vero? Allora, vi rendo subito la faccenda un tantino più complicata, perché in realtà gli elettroni non sono totalmente liberi di oscillare sotto l’impulso dell’onda incidente. Molti elettroni sono strettamente legati ai loro nuclei; altri elettroni sono più liberi di muoversi da un atomo ad un altro, ma sono comunque attratti dai nuclei nel loro insieme, così che se vengono spostati dal passaggio di un’onda elettromagnetica, lasciano un eccesso di carica positiva che tende a richiamarli alla posizione di partenza. Perciò, gli elettroni in un mezzo materiale tendono ad oscillare – qualora sollecitati – ad una frequenza naturale detta frequenza di plasma, che dipende dal numero di elettroni liberi per unità di volume. Si può calcolare che, per la maggior parte dei materiali, la frequenza di plasma vale 1016 – 1017 Hz, ovvero ricade tipicamente nel lontano ultravioletto. Molto più alta delle frequenze della luce visibile, ma più bassa di quelle dei raggi X.

Ed è proprio qui la chiave del diverso comportamento dell’indice di rifrazione nei due casi!

Infatti, nel caso della luce visibile, la frequenza incidente è minore della frequenza di plasma, perciò gli elettroni riescono a seguire le oscillazioni del campo dell’onda incidente in fase, cioè senza ritardo, e si verifica la situazione che abbiamo appena descritto. Viceversa, i raggi X hanno sempre una frequenza maggiore di quella di plasma del materiale in cui si propagano, quindi gli elettroni oscillano sì, ma in controfase – cioè sfasata di mezzo periodo – rispetto al campo dell’onda incidente, quindi questa volta la somma delle ondine prodotte dall’oscillazione degli elettroni risulterà in anticipo di ¼ di periodo. Di conseguenza, quando questa si sovrapporrà all’onda incidente, l’onda risultante sarà in leggero anticipo di fase, sempre senza cambiare frequenza. E pertanto, la velocità di fase vF diventerà maggiore di c e avremo un indice di rifrazione n = c/vF minore di 1…!

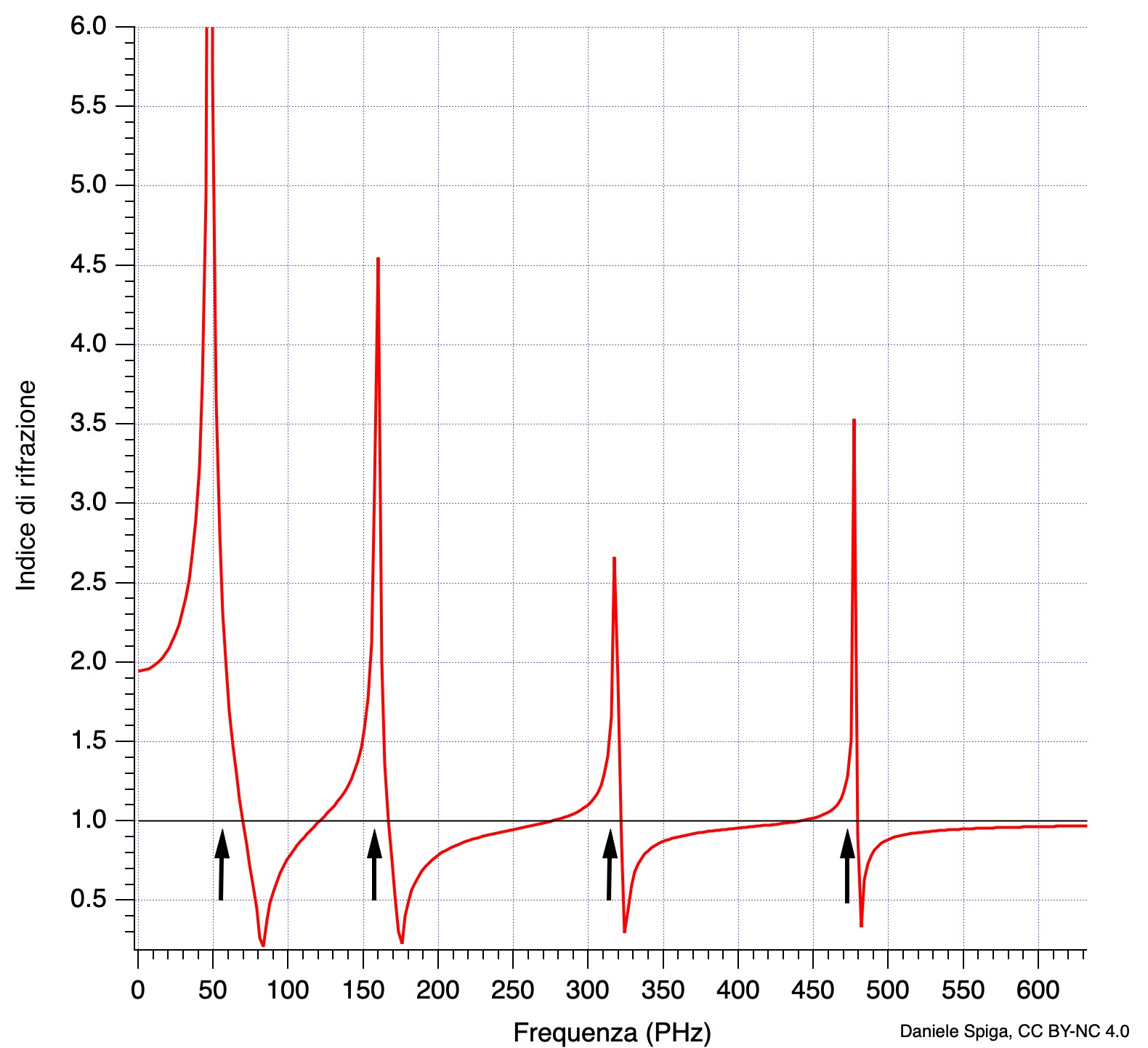
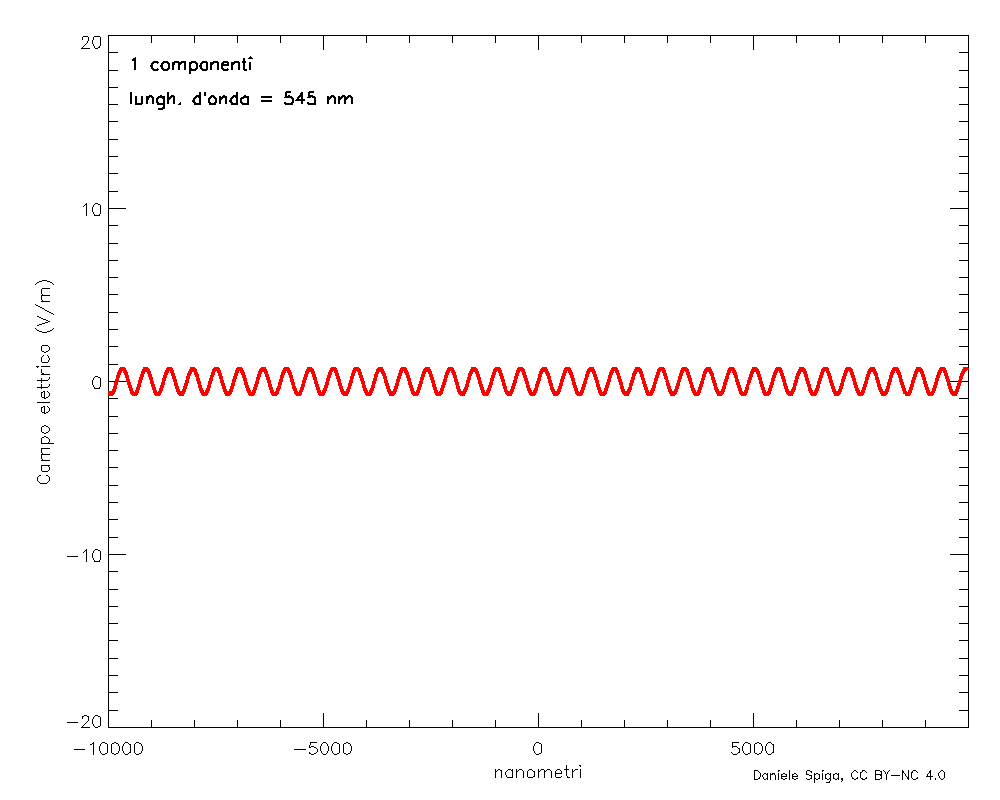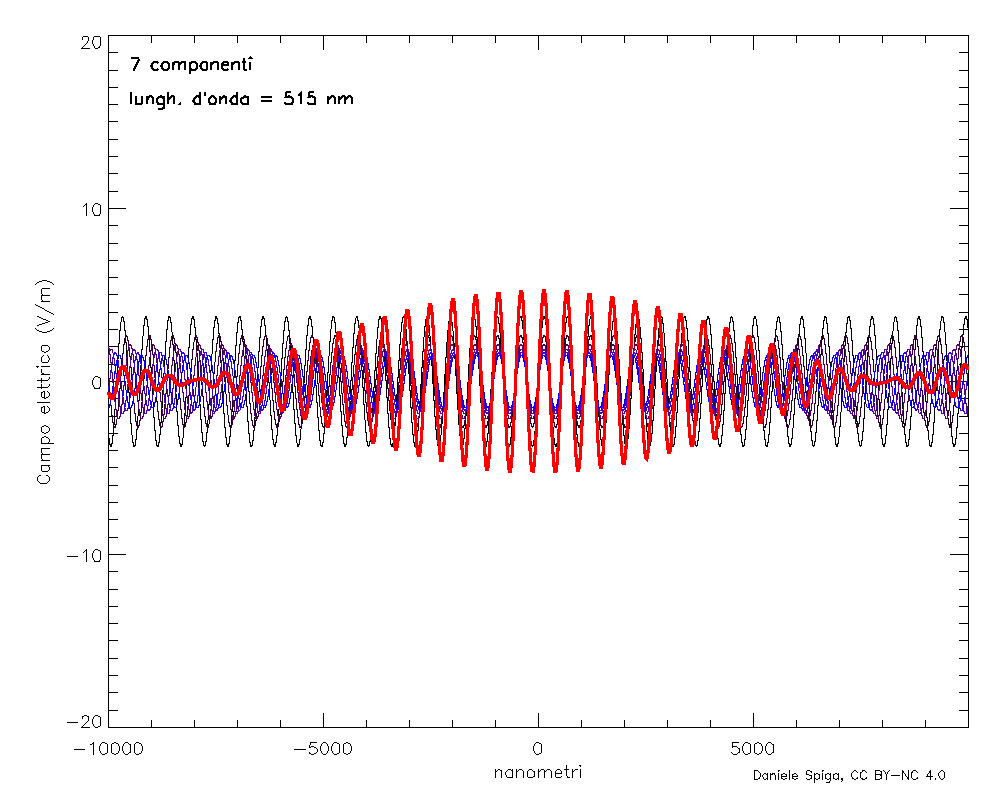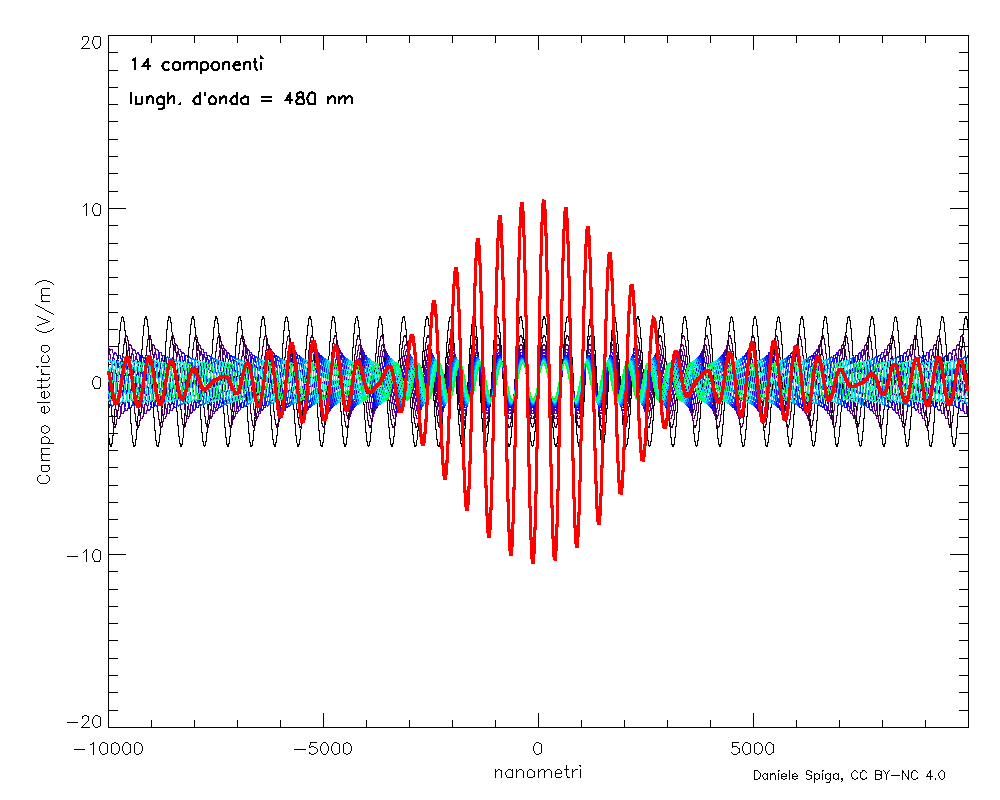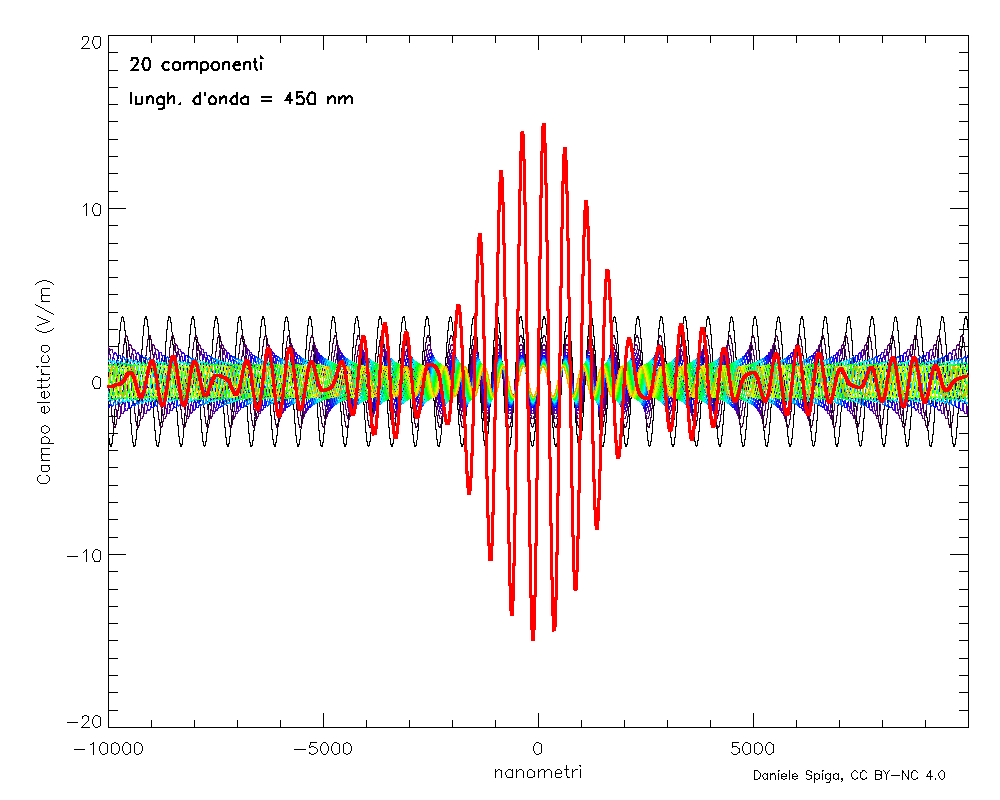
Manco a dirlo, in realtà ci sono ulteriori complicazioni di questo semplice modello (detto appunto modello di Drude, o modello del gas di elettroni). Infatti, anche gli elettroni legati ai nuclei, oppure gli stessi atomi all’interno delle molecole possono oscillare con le loro specifiche frequenze, e anche essi contribuiscono all’indice di rifrazione del materiale. Quando l’onda incidente supera non solo la frequenza di plasma, ma anche ciascuna di queste frequenze, gli oscillatori invertono bruscamente la loro fase, l’indice di rifrazione prima si impenna e subito dopo crolla bruscamente, per poi riprendere a crescere gradualmente con la frequenza. Un andamento tipico dell’indice di rifrazione è mostrato in Figura 6, in cui ciascuno dei “crolli” verticali corrisponde a una frequenza caratteristica del materiale. Tuttavia, se escludiamo questi salti, l’indice di rifrazione cresce sempre con la frequenza (compresi i tratti in cui n < 1). In ottica, tale fenomeno viene chiamato dispersione normale, per distinguerlo dai pochi intervalli in cui n decresce bruscamente con f (dispersione anomala). Ed è – come anticipavo alla fine della prima puntata – proprio la dispersione della luce che consente di rispondere alla seconda domanda: se i raggi X hanno un n < 1, come possono viaggiare più veloce della luce nel vuoto? Sorpresa: in realtà non lo fanno, per la semplice ragione che non esistono le onde perfettamente monocromatiche (come quella in Figure 2, 4 e 5) che abbiamo considerato finora; infatti, se esistessero, dovrebbero avere estensione e durata infinite, mentre le onde di cui tutti noi abbiamo esperienza hanno durata e estensione limitata nel tempo, come quella mostrata nella linea rossa di Figura 7. Parliamo allora più propriamente di pacchetti d’onda, e sono sicuro che – senza averli chiamati così – tutti noi li conosciamo bene; chiunque abbia saltato sulle onde del mare (i classici “cavalloni”) sa che le creste delle onde si presentano a gruppi, seguiti da periodi di quiete più o meno lunghi. Ebbene: questi gruppi sono proprio dei pacchetti d’onda, che si possono descrivere matematicamente (Figura 7) come la sovrapposizione di un grande numero di onde monocromatiche di frequenze diverse. Più ampia è la banda di frequenze che sovrapporremo, più stretto sarà il pacchetto, e viceversa. La luce naturale, quella bianca per intenderci, contiene molte frequenze e perciò i suoi pacchetti d’onda sono stretti impulsi di qualche micron, mentre un laser, che è molto più
monocromatico, ha dei pacchetti d’onda che possono arrivare oltre il chilometro. Ma in tutti i casi, l’energia (e quindi l’informazione) trasportata dall’onda è associata al pacchetto nel suo insieme e non alle singole creste delle onde!

Non ne siete convinti? Allora, pensateci un attimo: quanta informazione riuscite a trasportare con un’onda radio perfettamente monocromatica? Pochissima: giusto la frequenza e l’ampiezza, i due numeri che la definiscono completamente. È solo quando introduciamo la modulazione dell’onda, cioè creiamo degli impulsi dentro di essa come quelli in Figura 7, che riusciamo a trasportare molte più informazioni (come la musica, o il notiziario della nostra stazione radio preferita, o le immagini della televisione…).

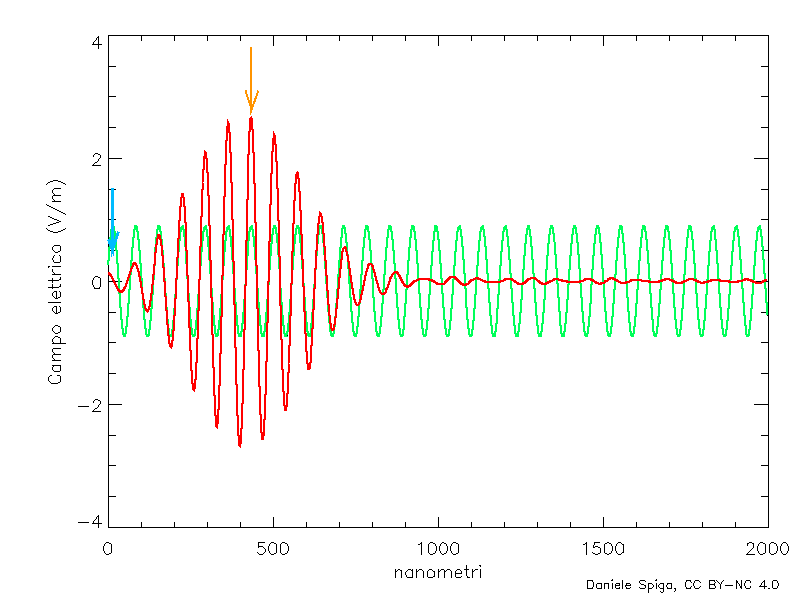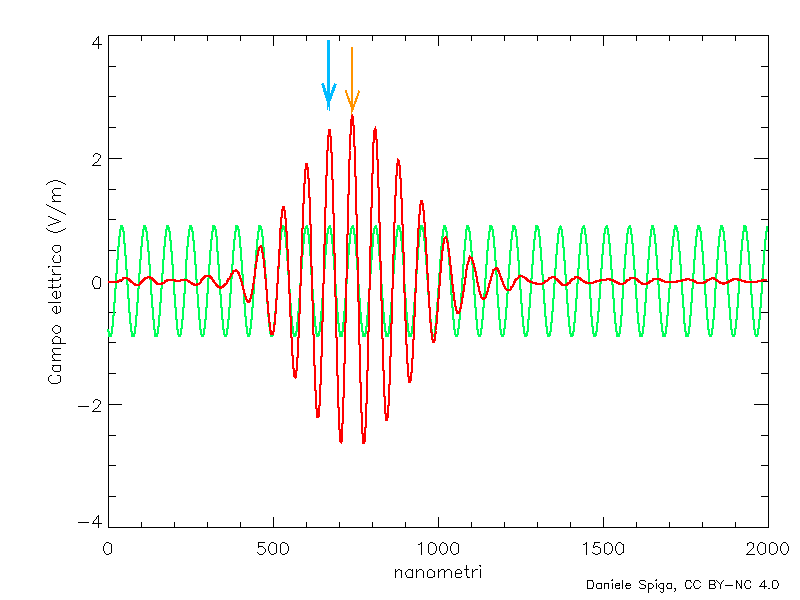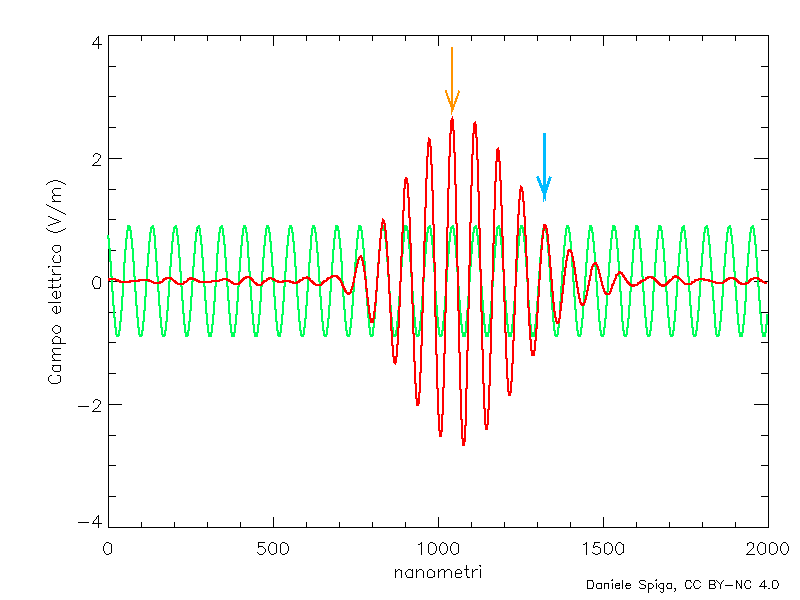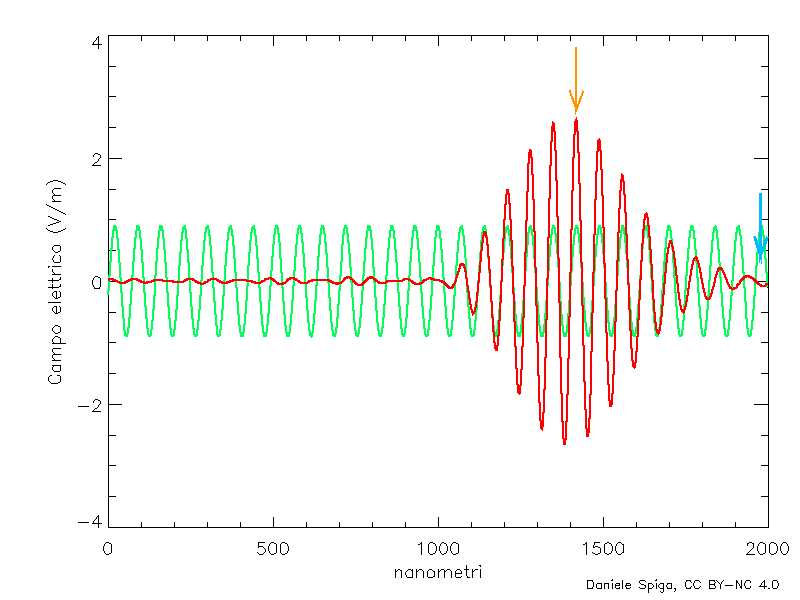
Ma ora… non abbiamo detto che per effetto della dispersione, la velocità di fase delle singole onde monocromatiche varia con la frequenza? E quindi, a che velocità si sposterà il pacchetto d’onda nel suo insieme (la cosiddetta velocità di gruppo, vG)? Qui succede qualcosa di completamente inatteso: in un mezzo dispersivo, in condizioni di dispersione normale[3], la velocità di gruppo è sempre inferiore a quella di fase, cioè il pacchetto nel suo insieme si sposta più lentamente delle creste delle onde (Figura 8), e anche se vF > c, avremo sempre vG < c. Questo comporta che l’energia trasportata dalla luce nel mezzo – e l’informazione che possiamo codificare in essa – non potrà mai superare quella che si ha nel vuoto. Possiamo tirare un sospiro di sollievo: anche per i raggi X, la relatività è salva!

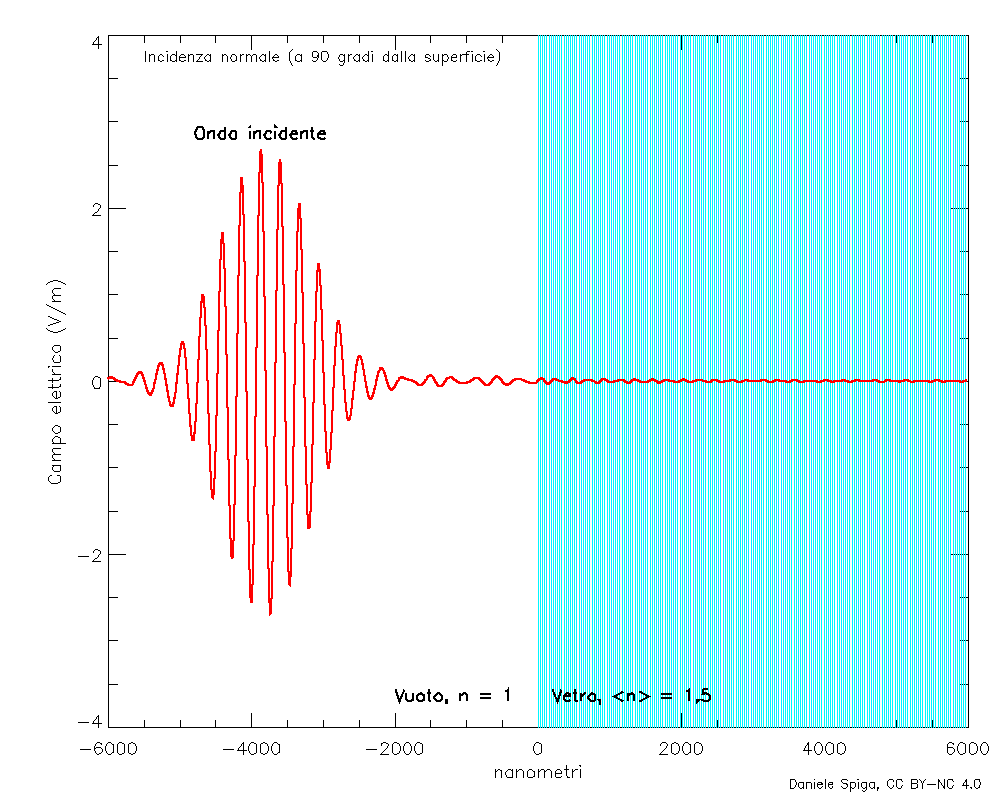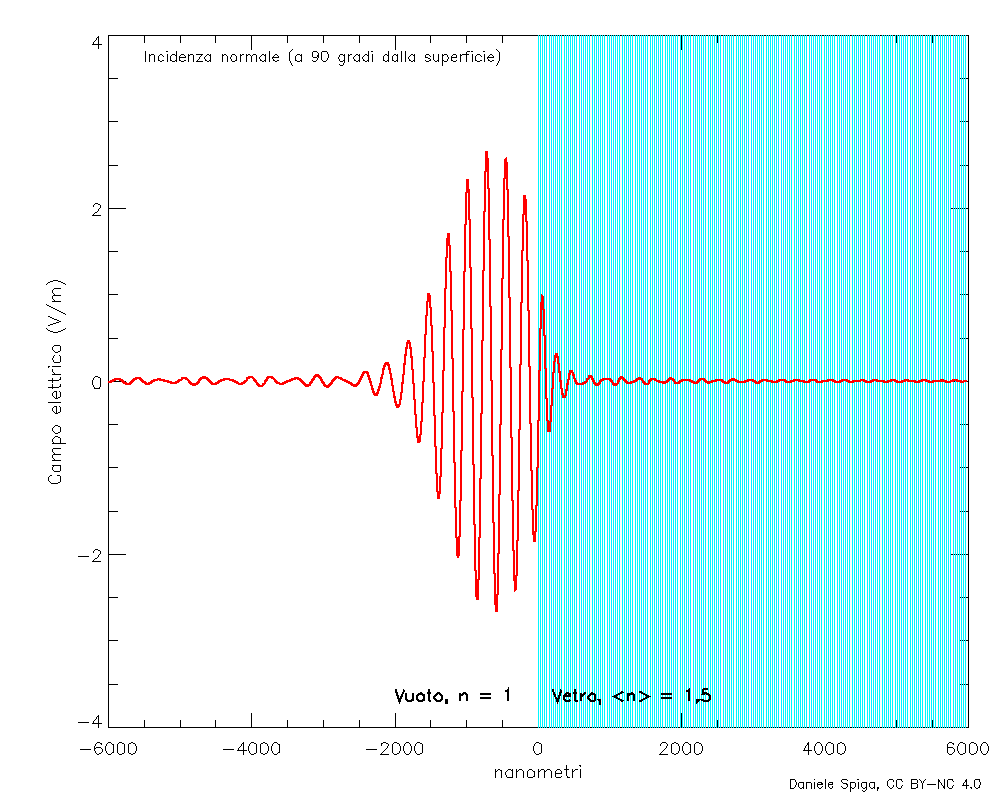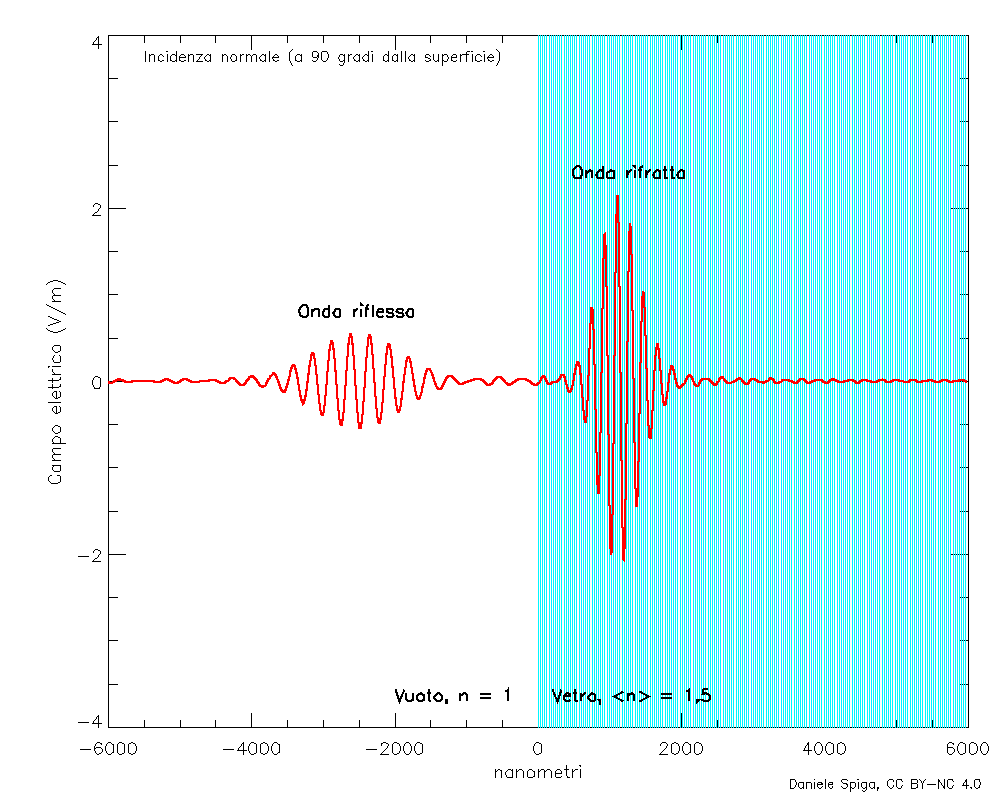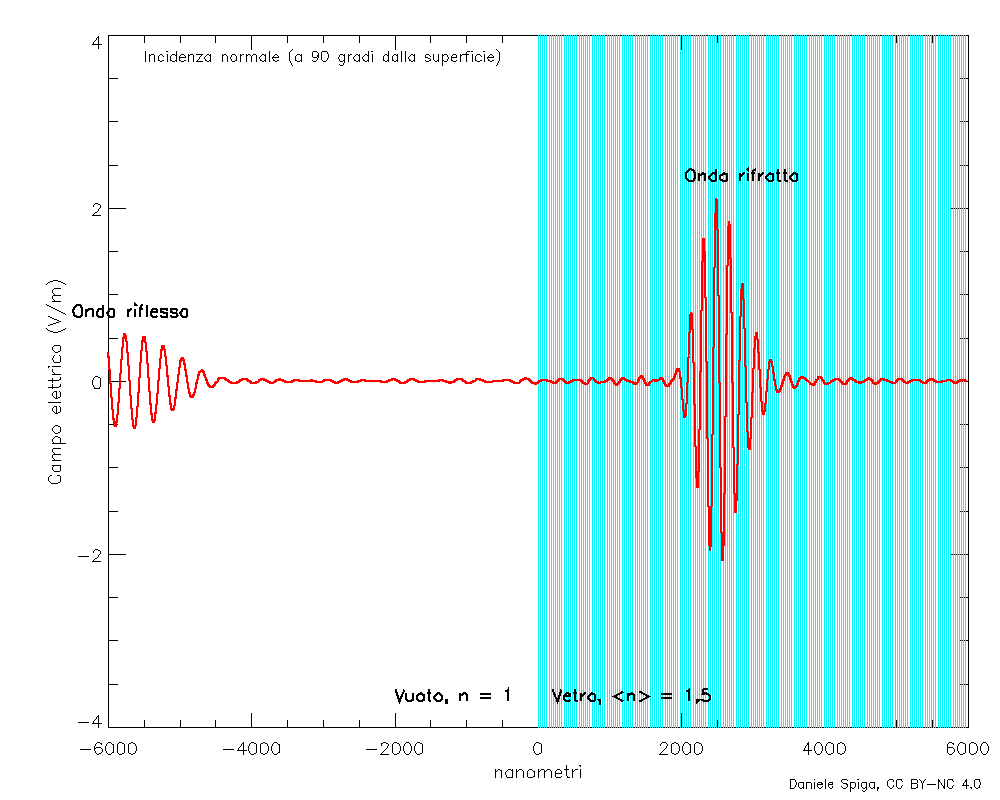
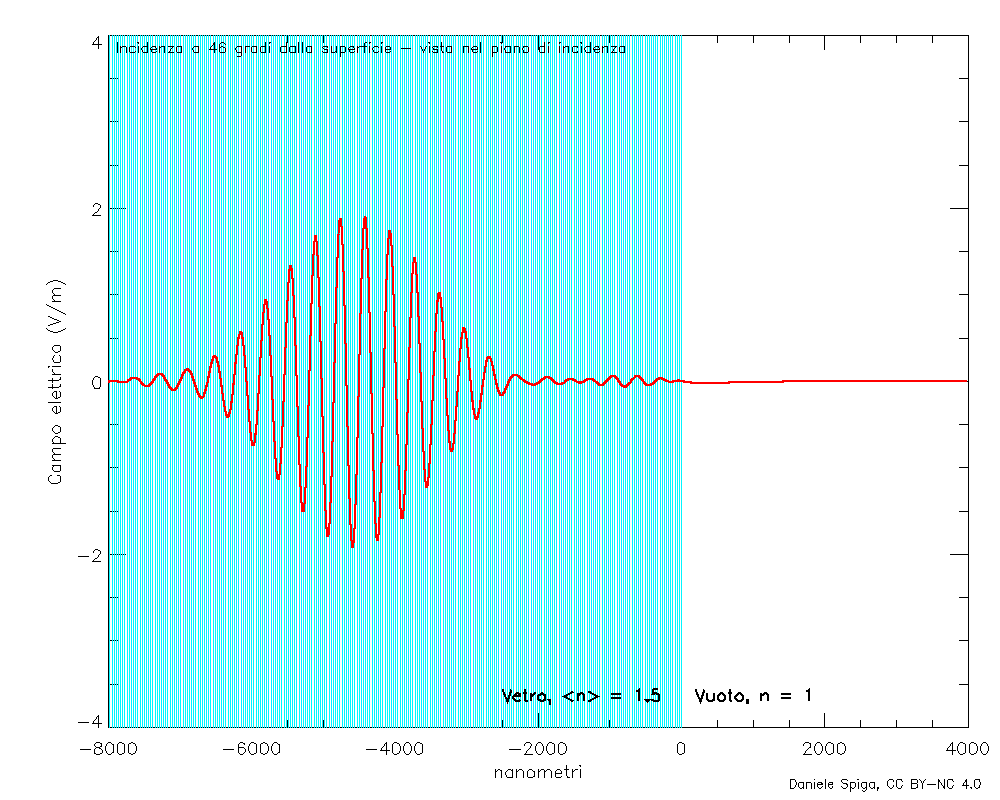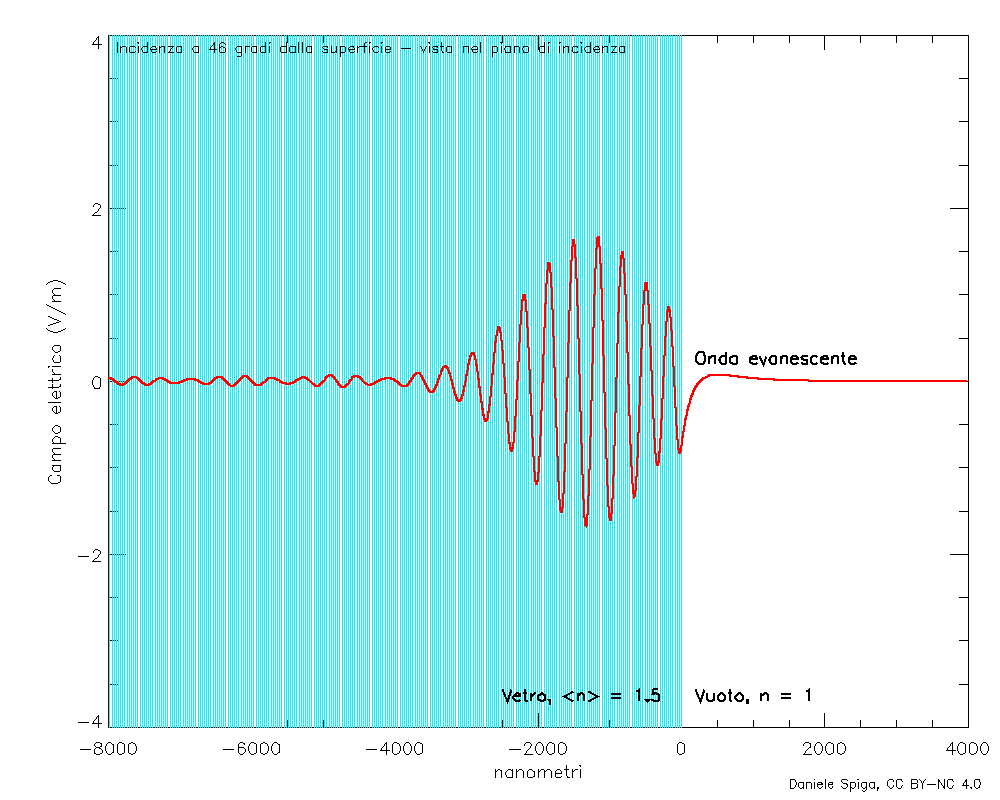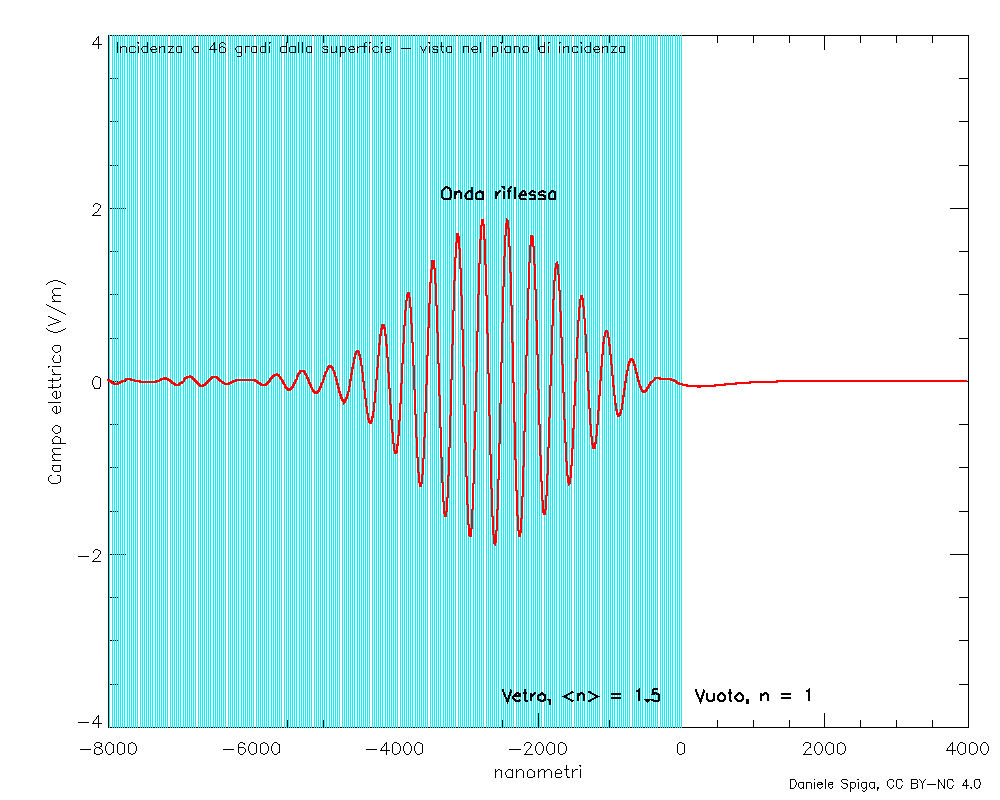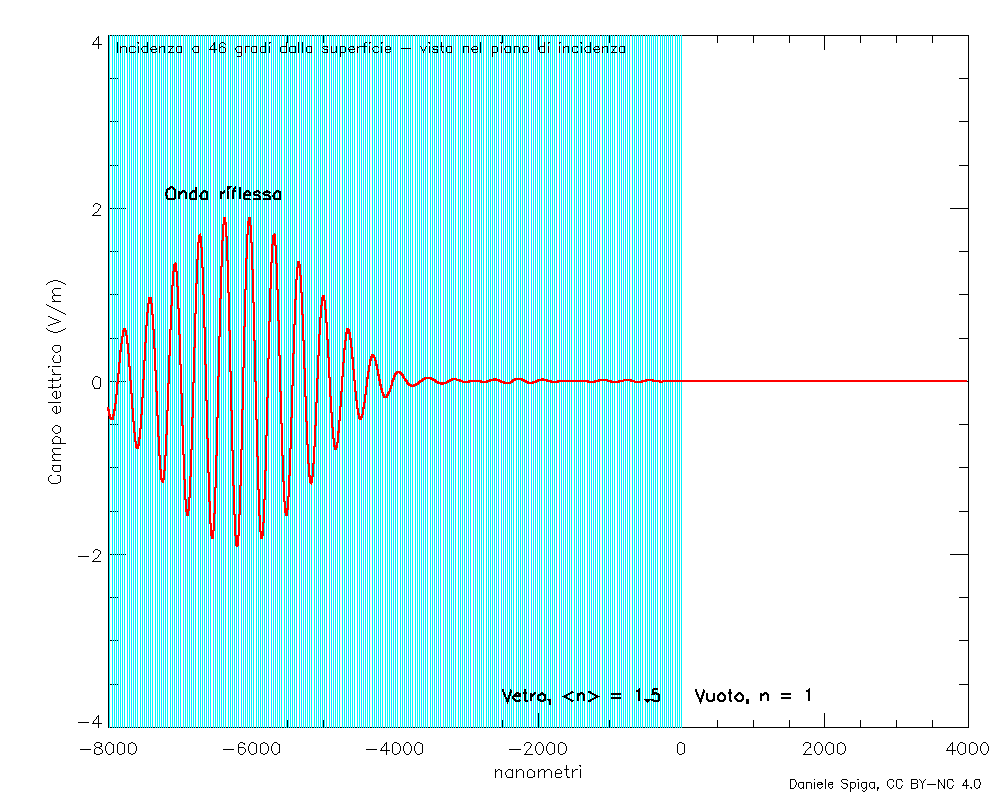
E, naturalmente, sovrapponendo tante onde monocromatiche che, oltre a rifrangersi come quelle in Figura 4, si riflettono, possiamo anche visualizzare il comportamento completo di un pacchetto d’onde quando incide su un mezzo materiale (Figura 9).

            Dopo avere compreso anche questo aspetto, nel prossimo episodio capiremo come si può utilizzare la riflessione totale dei raggi X per focalizzarli. Ovviamente, dovremo lavorare in incidenza radente, il che rende la geometria degli specchi per telescopi X molto peculiare. Ma, nel frattempo, non perdiamo di vista l’indice di rifrazione nei raggi X, perché le sue pazzie non finiscono qui. Ci torneremo in seguito, e le sorprese non mancheranno.

[1] In realtà, non sono solo i raggi X ad avere un indice di rifrazione inferiore a 1. Ad esempio, nella propagazione dei segnali radio in una guida d’onda la velocità di fase è regolarmente maggiore di c.

[2] Se vi interessano i calcoli in dettaglio, consultate il bellissimo capitolo 8 dell’Ottica di Bruno Rossi (sì, lo stesso che ha inventato l’astronomia X insieme a Riccardo Giacconi).

[3] Per gli irriducibili che si staranno chiedendo (giustamente): e se siamo in dispersione anomala? Risposta: in teoria la velocità di gruppo sarebbe maggiore di quella di fase, e quindi maggiore di c, ma in pratica il problema non si pone perché in corrispondenza alle frequenze di dispersione anomala con n < 1 di solito si verifica un forte assorbimento da parte del materiale.

Figura 1: James C. Maxwell (1831-1879) fu il primo a predire l’esistenza di onde nel campo elettromagnetico che si propagano alla velocità della luce (da Wikipedia, immagine di pubblico dominio).
Figura 1: James C. Maxwell (1831-1879) fu il primo a predire l’esistenza di onde nel campo elettromagnetico che si propagano alla velocità della luce (da Wikipedia, immagine di pubblico dominio).
Figura 2: schema di un’onda elettromagnetica sinusoidale che entra in un mezzo materiale, viaggiando verso destra (adattato da Supermanu, via Wikimedia Commons, CC BY-SA 3.0).
Figura 2: schema di un’onda elettromagnetica sinusoidale che entra in un mezzo materiale, viaggiando verso destra (adattato da Supermanu, via Wikimedia Commons, CC BY-SA 3.0).
Figura 3: ognuna delle componenti monocromatiche in cui è stato suddiviso un raggio di luce bianca è, con buona approssimazione, un’onda sinusoidale (crediti: D. Spiga).
Figura 3: ognuna delle componenti monocromatiche in cui è stato suddiviso un raggio di luce bianca è, con buona approssimazione, un’onda sinusoidale (crediti: D. Spiga).

Figura 4: rifrazione di un’onda elettromagnetica (lunghezza d’onda = 400 nm) dall’aria al vetro. Si noti come nella rifrazione la diminuzione della velocità di fase sia dovuta alla diminuzione della lunghezza d’onda di un fattore pari al rapporto tra gli indici di rifrazione, mentre la frequenza rimane inalterata (crediti: D. Spiga).
Figura 4: rifrazione di un’onda elettromagnetica (lunghezza d’onda = 400 nm) dall’aria al vetro. Si noti come nella rifrazione la diminuzione della velocità di fase sia dovuta alla diminuzione della lunghezza d’onda di un fattore pari al rapporto tra gli indici di rifrazione, mentre la frequenza rimane inalterata (crediti: D. Spiga).
Figura 5: rallentamento di un’onda elettromagnetica per rifrazione (n>1). L’inserimento di un sottile strato di vetro genera un’onda secondaria in ritardo di fase di ¼ di periodo, ritardando la fase dell’onda trasmessa. Al limite di infiniti strati infinitamente sottili, si ottiene una riduzione della lunghezza d’onda e della velocità di fase nel vetro (crediti: D. Spiga).
Figura 5: rallentamento di un’onda elettromagnetica per rifrazione (n>1). L’inserimento di un sottile strato di vetro genera un’onda secondaria in ritardo di fase di ¼ di periodo, ritardando la fase dell’onda trasmessa. Al limite di infiniti strati infinitamente sottili, si ottiene una riduzione della lunghezza d’onda e della velocità di fase nel vetro (crediti: D. Spiga).
Figura 6: Andamento dell’indice di rifrazione con la frequenza in un ipotetico materiale con frequenze di risonanza indicate in PHz (1 petahertz = 1015 hertz). Nell’ultimo tratto ad alta frequenza, l’indice di rifrazione rimane stabilmente minore di 1 (crediti: D. Spiga).
Figura 6: Andamento dell’indice di rifrazione con la frequenza in un ipotetico materiale con frequenze di risonanza indicate in PHz (1 petahertz = 1015 hertz). Nell’ultimo tratto ad alta frequenza, l’indice di rifrazione rimane stabilmente minore di 1 (crediti: D. Spiga).
Figura 7: un pacchetto d’onda generato sovrapponendo onde sinusoidali in una banda di lunghezze d’onda 450-550 nm (crediti: D. Spiga).
Figura 7: un pacchetto d’onda generato sovrapponendo onde sinusoidali in una banda di lunghezze d’onda 450-550 nm (crediti: D. Spiga).
Figura 8: simulazione di propagazione in un mezzo dispersivo di un pacchetto d’onda (rosso) ottenuto sovrapponendo 100 componenti sinusoidali distribuite attorno a una frequenza principale (in verde). La freccia blu (velocità di fase) segue lo spostamento di una cresta, la freccia arancio (velocità di gruppo) segna il punto più alto del profilo del pacchetto. La velocità di fase è proporzionale alla radice quadrata della lunghezza d’onda e il valore medio dell’indice di rifrazione è 1.7 (crediti: D. Spiga).
Figura 8: simulazione di propagazione in un mezzo dispersivo di un pacchetto d’onda (rosso) ottenuto sovrapponendo 100 componenti sinusoidali distribuite attorno a una frequenza principale (in verde). La freccia blu (velocità di fase) segue lo spostamento di una cresta, la freccia arancio (velocità di gruppo) segna il punto più alto del profilo del pacchetto. La velocità di fase è proporzionale alla radice quadrata della lunghezza d’onda e il valore medio dell’indice di rifrazione è 1.7 (crediti: D. Spiga).
Figura 9: simulazione della rifrazione/riflessione di un pacchetto d’onda in incidenza normale su un vetro. Si noti che nel vuoto il pacchetto si propaga senza cambiare forma, mentre all’ingresso nel vetro, che è un mezzo dispersivo, la velocità di fase supera la velocità di gruppo - come si verifica in Figura 8 - e il pacchetto inizia a sparpagliarsi. La velocità di fase nel vetro è proporzionale alla radice quadrata della lunghezza d’onda e il valore medio dell’indice di rifrazione è 1.5 (crediti: D. Spiga).
Figura 9: simulazione della rifrazione/riflessione di un pacchetto d’onda in incidenza normale su un vetro. Si noti che nel vuoto il pacchetto si propaga senza cambiare forma, mentre all’ingresso nel vetro, che è un mezzo dispersivo, la velocità di fase supera la velocità di gruppo – come si verifica in Figura 8 – e il pacchetto inizia a sparpagliarsi. La velocità di fase nel vetro è proporzionale alla radice quadrata della lunghezza d’onda e il valore medio dell’indice di rifrazione è 1.5 (crediti: D. Spiga).
Figura 10: simulazione della riflessione totale di un pacchetto d’onda all’interno del vetro, a 46° dalla superficie. All’esterno del vetro non si ha formazione di un’onda viaggiante, ma solo di un’onda evanescente che decresce esponenzialmente con la distanza dalla superficie.
Figura 10: simulazione della riflessione totale di un pacchetto d’onda all’interno del vetro, a 46° dalla superficie. All’esterno del vetro non si ha formazione di un’onda viaggiante, ma solo di un’onda evanescente che decresce esponenzialmente con la distanza dalla superficie.

Tag