La curiosità del mese a cura di Gianluigi Filippelli

Il modello di Ising: le basi fisiche delle reti neurali
Il premio Nobel per la Fisica 2024 è stato assegnato a John Hopfield e Geoffrey Hinton
“per le fondamentali scoperte e invenzioni che hanno permesso alle macchine di imparare attraverso reti neurali artificiali.”
In particolare il fisico teorico John Hopfield, dopo aver modellizzato il comportamento cooperativo dell’emogoblina, ha lavorato su un modello che si è rivelato piuttosto versatile, applicandolo al funzionamento di una memoria.
Il modello, che, come vedremo, fu sviluppato in un altro ambito, è il
cosiddetto modello di Ising.
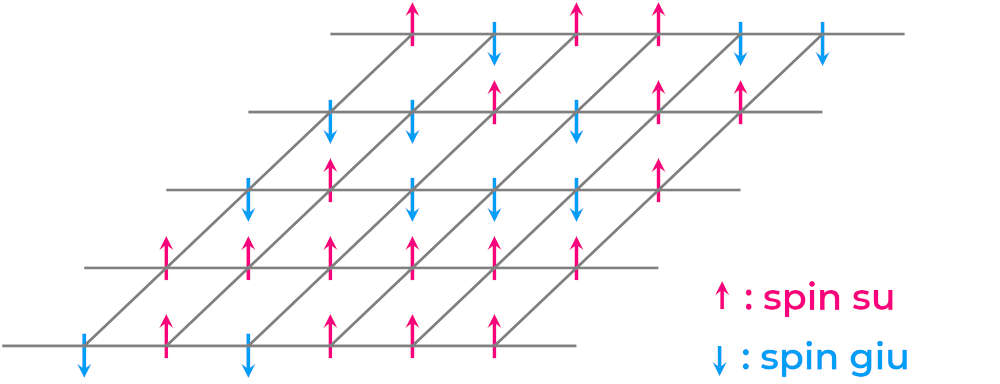
Catene di spin
Il modello venne realizzato da Wilhelm Lenz, che successivamente lo assegnò al suo studente Ernst Ising, da cui il nome. Quest’ultimo, nel 1924, trovò una soluzione completa nel caso monodimensionale, descritta nella sua tesi. La struttura del modello, che riprende la matematica delle reti, è abbastanza semplice.
Il modello matematico, infatti, descrive una catena di spin in cui troviamo un termine relativo all’interazione elettromagnetica tra due diversi spin e un termine che rappresenta una perturbazione esterna.
Quest’ultima, nel caso più generale, varia da nodo a nodo. Nel caso monodimensionale, il modello non presenta alcuna transizione di fase, cosa che invece avviene a dimensioni superiori. Non siamo, però, qui
per tracciare una storia completa del modello: basti sapere che ha avuto diverse applicazioni, anche fuori dalla fisica: nello studio del magnetismo, della dinamica dei gas, per descrivere, come “detto”, catene e reticoli di spin, nella descrizione delle transizioni di fase quantistiche, nelle neuroscienze e nello sviluppo delle reti neurali.
Il modello di Hopfield e Amari
Il primo uso in tal senso risale al 1972 quando l’ingegnere matematico Shun’ichi Amari modificò opportunamente il modello di Ising per descrivere il funzionamento di una memoria. Cosa che fece 10 anni più tardi anche Hopfield.
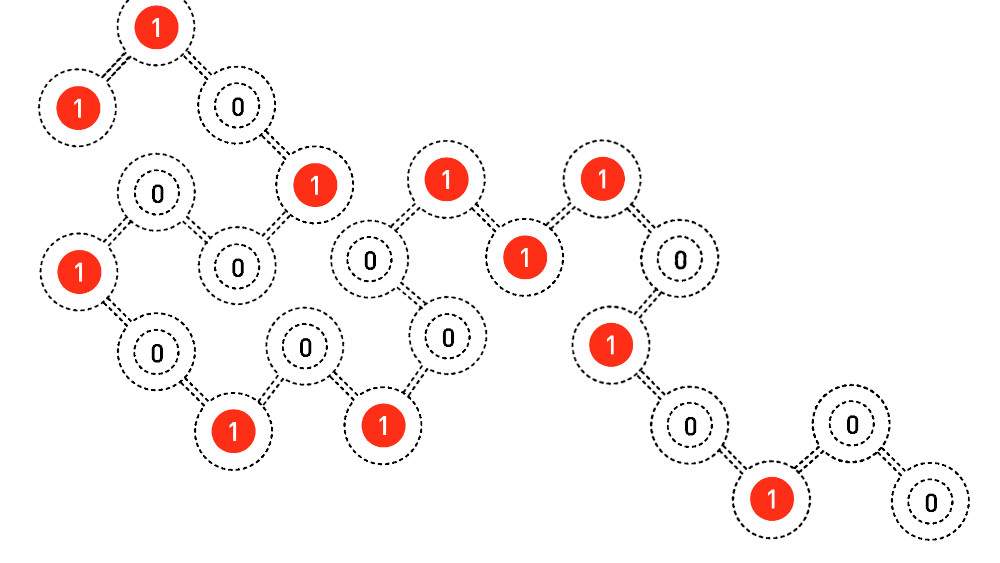
Dal punto di vista matematico il modello di Hopfield e Amari non è molto diverso da quello di Ising. In pratica il modello descrive in che modo i nodi, detti, ovviamente, “neuroni”, interagiscono uno con l’altro. A ciascun nodo viene poi associata una funzione di attivazione, che ha valore 0 se il “neurone” non è attivo, e valore 1 se il “neurone” è attivo. La perturbazione esterna, invece, diventa il bias, ovvero i preconcetti introdotti all’interno della rete neurale. Due anni più tardi Hopfield migliorò ulteriormente il modello, sostituendo la funzione di attivazione dei neuroni, a due valori, con una funzione che rappresenta, invece, la probabilità di attivazione, passando quindi da valori discreti a un intervallo di valori compresi tra 0 e 1. La successiva miglioria arrivò nel 1985 grazie al gruppo di ricerca di Hinton.
Uno dei suoi collaboratori, Terry Sejnowski, era un fisico. Il gruppo diede due migliorie sostanziali al modello. La prima era legata all’uso della termodinamica di Boltzman per la descrizione delle funzioni di attivazione, la seconda all’uso di due (e successivamente più) reti neurali innestate una dentro l’altra, distinguendo così tra le reti neurali visibili e quelle nascoste. Questo approccio permetteva di immagazzinare una maggiore quantità di informazioni, e, soprattutto, aveve una maggiore velocità di calcolo.
Finisce qui questo racconto del ruolo della fisica, e di un particolare modello fisico, nei primi passi delle attuali reti neurali.
L’appuntamento è a una futura Astrocuriosità per raccontare in che modo le reti neurali sono utilizzate in astronomia.