La curiosità del mese a cura di Daniele Spiga

A chi di noi non è capitato di lasciare le proprie cose sulla spiaggia, a una discreta distanza dalla battigia, andare a nuotare qualche ora, per poi tornare e scoprire che il mare si è portato via tutto? Come …? A nessuno …? Allora sono proprio io che sono sprovveduto… comunque avete capito che oggi parliamo delle maree. Due volte al giorno, su tutta la Terra, il livello dei mari si alza e si abbassa in misura variabile. Sono un fenomeno importantissimo per la navigazione, ma la loro causa è rimasta un mistero fino all’età moderna. Riuscirono a mettere in crisi perfino il grande Galileo che le citò – sbagliando, ma anche i migliori sbagliano! – come prova della rotazione terrestre, argomento che gli stava molto a cuore. Quando Newton scoprì la legge di gravitazione universale, si comprese subito che era la gravità della Luna (e in misura minore, anche quella del Sole) ad attrarre tutta la massa dei mari e degli oceani verso di sé, opponendosi alla gravità terrestre. Poiché la Terra compie una rotazione sul suo asse in un tempo molto minore di quello in cui la Luna completa un’orbita intorno alla Terra, noi terrestri vediamo il rigonfiamento mareale muoversi da est a ovest, come se fosse un’onda lunghissima. È quella che chiamiamo onda di marea.
Ma non è così semplice. Mentre la Terra ruota, l’onda di marea “gratta” contro il fondale oceanico (attrito delle maree) e quindi è sempre un po’ in ritardo rispetto alla Luna. Inoltre, a volte i mari sono chiusi in mezzo alle terre emerse (pensate al nostro Mediterraneo, o al mar Baltico) che ritardano, smorzano e deviano l’onda di marea; oppure, viceversa, infrangendosi contro i continenti la marea viene riflessa oppure viene “intrappolata” nei golfi, raggiungendo altezze di una decina di metri, come nella baia di Fundy in Canada. E si tratta di un fenomeno ben più che suggestivo: nel II secolo a.C., l’astronomo greco Ipparco di Nicea (a cui già dobbiamo: il concetto di magnitudine stellare, il primo catalogo stellare, la scoperta della precessione degli equinozi, la prima stima della distanza della Luna, la trigonometria, …) osservò che le maree nell’Oceano Atlantico (Figura 1) sono in media più alte che nell’Oceano Indiano, e comprese che ciò era dovuto alla presenza di un ampio continente che rifletteva l’onda di marea verso l’Europa. Quel geniaccio di Ipparco aveva scoperto l’America 17 secoli prima di Colombo, e senza nemmeno prendere una caravella.
Ma se pensiamo che le stranezze finiscano qui, dovremo ricrederci: ad esempio, come la mettiamo col fatto che ogni giorno ci sono due basse maree e due alte maree, mentre la Luna passa sopra la nostra testa una sola volta al giorno? Va benissimo che l’alta marea segua di poco la culminazione della Luna, ma allora perché l’alta marea successiva arriva circa 12 ore e mezza dopo, mentre la Luna è dalla parte opposta della Terra?
Fu il matematico e reverendo inglese John Wallis (1616 – 1703) a fornire la spiegazione, semplice ma controintuitiva, di questo strano fatto. Noi siamo soliti dire che la “Luna gira intorno alla Terra”, ma non è corretto; in realtà, Luna e Terra ruotano entrambe intorno al loro centro di massa comune (il punto O in Figura 2). Date le ragguardevoli massa e distanza del nostro amato satellite, il centro di massa è a una profondità di soli 1700 km sotto la superficie terrestre. Perciò, la parte opposta della Terra C rispetto alla Luna è 11000 km più lontana dal centro di rotazione rispetto ad A, la parte rivolta verso la Luna. Adesso ricordiamoci che in un sistema rotante compaiono diverse forze apparenti, tra cui la famosa forza centrifuga, che ha la proprietà di aumentare in proporzione alla distanza dal centro di rotazione (e basta fare un giro su una giostra per rendersene conto).
A questo punto, avete capito: è la maggiore forza centrifuga dovuta alla rotazione del sistema Terra-Luna che causa l’innalzamento della marea dalla parte opposta della Luna. Facendo un po’ di conti, si verifica che la somma delle forze (gravità Terra + gravità Luna + forza centrifuga) nel punto C è circa esattamente uguale a quella nel punto A e leggermente minore di quella nel punto B, e che la differenza tra l’accelerazione totale in A e in B è data dalla formula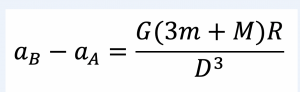
dove G è la solita costante di gravitazione universale, m la massa della Luna, M quella della Terra, R il raggio terrestre e D la distanza Terra-Luna. Il fatto che sia proporzionale alla massa ma inversamente proporzionale al cubo della distanza … ci dice che nelle maree la distanza conta molto più della massa. Ad esempio, il Sole è molto più massiccio della Luna, ma la sua distanza dalla Terra è tale che il suo contributo alle maree è inferiore. Attualmente, con la Luna a 384000 km e 27.3 giorni di periodo orbitale, la differenza di accelerazione tra i punti A e B è piccola (circa 5´10-5 m/s2, contro 9.8 m/s2 di accelerazione di gravità terrestre), ma sufficiente in media a sollevare gli oceani … di poco più di un metro. Ma 4 miliardi di anni fa, quando la Luna era 10 volte più vicina alla Terra, la rotazione terrestre si completava in 5 ore circa, e il sistema Terra-Luna completava un’orbita in 22 ore circa… le maree dovevano avere la terrificante ampiezza di oltre un chilometro!
E, attenzione: le maree hanno effetto su tutta la massa della Terra… noi lo osserviamo sui mari perché i fluidi si deformano istantaneamente, ma lo fa anche la Terra “solida”, anche se molto più lentamente, e quindi in misura molto minore. Ma mentre la Terra ruota, l’attrito risultante dalla deformazione della Terra e soprattutto quello delle maree sui fondali oceanici dissipa un sacco di energia rotazionale: con il duplice effetto di rallentare la rotazione terrestre (2 millisecondi/secolo) e allontanare la Luna (3.8 cm/anno)!
Quanto detto non vale solo per la Terra e la Luna, ma per qualunque coppia di oggetti che si muovano sotto l’effetto della gravità reciproca. Chiamiamo questa combinazione di gravità e forza centrifuga (due facce della stessa medaglia, in realtà) forze di marea. Ebbene, le forze di marea stirano in lunghezza e strizzano i fianchi, proprio come un vestito stretto in vita… e quello che potrebbe sembrare un gradevole effetto snellente diventa catastrofico se supera un certo limite, detto limite di Roche, ma a questo dedicheremo un’altra puntata. Si tratta comunque di un comportamento inatteso perché la nostra esperienza quotidiana ci suggerisce che la gravità non faccia altro che attrarre, mentre il suo vero effetto, come ci ha insegnato Einstein, è quello di deformare lo spazio. Anche la Terra esercita delle forze di marea sulla Luna, che danno a quest’ultima una forma leggermente allungata in direzione della Terra. Così, a furia di dissipare energia di rotazione deformandosi in continuazione nelle forze di marea prodotte dalla Terra e dal moto orbitale, la Luna ha rallentato progressivamente la rotazione intorno al suo asse fino a raggiungere la sincronia con il suo moto di rivoluzione. Questo fenomeno, chiamato rotazione sincrona o blocco mareale (in inglese: tidal locking) è il motivo per cui la Luna rivolge verso di noi sempre la stessa faccia. Il processo sarà completo quando la Terra, a furia di rallentare la sua rotazione per l’attrito delle maree, rivolgerà anche lei sempre la stessa faccia verso la Luna. Dovremmo arrivarci fra un tempo incredibilmente lungo… forse 50 miliardi di anni, quando il Sole sarà già morto e ridotto a una nana bianca da 45 miliardi di anni. E, ammesso che la Terra e l’Umanità siano sopravvissute in qualche modo a tale catastrofe, di sicuro il lato della Terra con vista sulla Luna (anche più lontana di quasi una volta e mezza, vedi Figura 3) sarà richiestissimo sul mercato degli immobili…!
Anche la maggior parte delle lune di Giove e Saturno, e molti pianeti extrasolari che orbitano molto vicino alla loro stella, sono tutti in rotazione sincrona. Plutone e Caronte (Figura 4) sono già in blocco mareale completo, e rivolgono la stessa faccia l’uno all’altro mentre si muovono su un’orbita quasi perfettamente circolare intorno al loro centro di massa. Anche il pianeta Mercurio risente delle forze di marea del Sole, ma la sua orbita è fortemente eccentrica e questo rende tutto più complicato.
Ma ci sono dei casi più insoliti: al contrario della Luna, il satellite Phobos orbita intorno a Marte in un tempo minore (7 ore e mezza) di un periodo di rotazione di Marte (24 ore e mezza), quindi le forze mareali lo fanno avvicinare a Marte di circa 2 cm all’anno. Va ancora peggio a Tritone, satellite di Nettuno, che orbita in senso contrario alla rotazione del pianeta, così che le maree su Nettuno lo fanno avvicinare di ben 9 cm/anno… e come finirà la storia lo scopriremo in una prossima puntata.
Il caso di Io, una delle quattro lune maggiori di Giove (Figura 5), è particolarmente interessante perché pur essendo in rotazione sincrona, ha un’orbita un po’ eccentrica, quindi è soggetta a variazione nelle forze mareali dell’enorme pianeta che la deformano di più di 100 m ad ogni orbita! E a questo “maltrattamento” si aggiungono le sue lune sorelle maggiori, Ganimede e Europa, che stirano e strizzano Io ogni volta che le passano vicino. E anche su questo torneremo più avanti.
Ma da oggi in poi, quando guarderete la Luna, o il mare, o andrete in America, o sentirete la forza centrifuga su una giostra, o meglio ancora… guarderete la Luna stando su una giostra in riva al mare in America: pensate alla Fisica che collega tutte queste cose, in una maniera davvero incredibile.





