La curiosità del mese a cura di Daniele Spiga

Quando Galileo, osservando le oscillazioni del pendolo, fece la grande scoperta, per prima cosa andò a dar la notizia al Granduca di Toscana.
“Eccellenza,” gli disse “ho scoperto che il mondo si muove”.
“Ma davvero?” fece il Granduca, meravigliato e anche un po’ allarmato. “E come l’avete scoperto?”
“Col pendolo”.
“Accidenti! Colpendolo con che cosa?”
Da Achille Campanile, “Vite degli Uomini Illustri” (1975, Rizzoli)
Questo divertente dialogo, in realtà, non ebbe mai luogo. L’esperimento, a cui scherzosamente si riferiva il grande scrittore umorista, fu in realtà realizzato da Léon Foucault nel 1851 a Parigi e fornì la prima prova diretta della rotazione terrestre. E che, guarda caso, si chiama pendolo di Foucault (Figura 1). Galileo cercò a lungo le prove che fosse la Terra a ruotare, non il cielo delle stelle fisse, ed erroneamente pensò che fossero le maree (leggi l’astrocuriosita’ di settembre 2021: “La marea che non ti aspettavi”). Le prova che gli dava definitivamente ragione sarebbe arrivata, per l’appunto, solo due secoli dopo la sua scomparsa.
Oggi siamo tutti sicuri che la Terra compia un giro sul suo asse in 23 ore, 56 minuti e 4 secondi (il giorno siderale). No, non sono esattamente 24 ore (giorno solare). I quattro minuti scarsi che mancano all’appello sono dovuti al fatto che la Terra si muove anche intorno al Sole e quindi la Terra deve ruotare di circa un grado in più ogni giorno per trovare il Sole nella stessa posizione rispetto ai suoi meridiani. Ma che sia proprio la Terra a ruotare ha innumerevoli conseguenze, una delle quali la abbiamo vista l’anno scorso: la Terra non è precisamente una sfera ma è schiacciata ai poli (leggi l’astrocuriosita` di giugno 2021: “La grande pera, ovvero il pianeta Terra”).
La causa dello schiacciamento polare (o, equivalentemente, del rigonfiamento equatoriale) è dovuto alla forza centrifuga che appare nel sistema di riferimento della Terra mentre ruota. Questa forza la sperimentiamo tutti su una giostra o quando svoltiamo su una strada, ed è il motivo per cui dobbiamo inclinare la bici verso l’interno della curva e gli pneumatici devono avere una buona aderenza sull’asfalto. La conoscono molto bene i pizzaioli, che fanno girare la pasta rapidamente per allargarla e renderla sottile. Quindi, la rotazione tende ad appiattire.
Viceversa, la gravità attira verso il centro da tutte le direzioni, quindi tende a sfericizzare. Non che ci riesca sempre, beninteso. Ce la fa solo se le masse in gioco sono abbastanza grandi da vincere le forze elettromagnetiche tra gli atomi che tendono a dare alla materia le forme più strane, come quelle che infatti possiedono gli asteroidi. I pianeti e i pianeti nani sono invece dominati dalla propria gravità, e se non ruotassero sarebbero sferici come gocce d’acqua in caduta libera (si parla infatti di “equilibrio idrostatico”).
In questo tira-e-molla tra forza centrifuga e gravità, la gravità ha quasi sempre la meglio, ed è per questo che non conosciamo pianeti piatti. La forma che assume una sfera schiacciata ai poli ha un nome in matematica: sferoide oblato. Bene, nell’Universo tutti gli oggetti auto-gravitanti e rotanti hanno questa forma. La piattezza è invece una spiccata proprietà delle pizze, con la notevole eccezione dei calzoni farciti.
Ora, se vi piace la matematica (se no, saltate pure questo paragrafo), potete calcolare facilmente la differenza tra i raggi polare ed equatoriale di uno sferoide oblato omogeneo di massa M e raggio medio R in equilibrio idrostatico (quindi, con le pizze non funziona), in rotazione abbastanza lenta con periodo T, usando la formula:
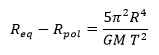
dove G è la famosa costante di gravitazione universale. Se proviamo ad applicarla, otteniamo che sulla Terra il raggio equatoriale sopravanza quello polare di circa 27 km.
Attualmente, la Terra (Figura 2) gira abbastanza lentamente, quindi la forza centrifuga è piuttosto debole rispetto alla sua gravità, ma è sufficiente a far sì che il raggio equatoriale sia maggiore di quello polare di appena 21 km (un po’ meno di quanto calcolato, ma è perché la Terra non è una sfera omogenea; è molto più densa al centro). Ma nello spazio ci sono cose che ruotano molto più velocemente della Terra… prendiamo il pianeta Saturno (Figura 3): ha una massa 95 volte quella della Terra, quindi ci aspetteremmo che la sua gravità sia enorme e lo renda perfettamente sferico. Ma Saturno è anche 9.45 volte più grande della Terra e soprattutto ruota sul suo asse in sole 10 ore e mezza. La sua velocità di rotazione è tale che all’equatore di Saturno la forza centrifuga è il 16% della gravità, e infatti… Saturno appare decisamente (10%) schiacciato ai poli. Giove, Urano, e Nettuno presentano appiattimenti un po’ meno marcati, ma comunque ben visibili.
E … se usciamo dal Sistema Solare? Ci sono altri esempi interessanti di distorsione rotazionale, ad esempio alcune stelle, specie se giovani e irrequiete. Il nostro Sole è una tranquilla stella di mezza età e fa un giro sul suo asse in ben 27 giorni. Ma prendiamo una delle stelle più luminose del cielo estivo: Vega (a Lyrae, cioè la stella più brillante della costellazione Lira), che fa un giro sul suo asse in sole 12.5 ore! Questo non è strano, visto che le stelle giovani non hanno ancora avuto il tempo di disperdere il loro momento angolare tramite il vento stellare. Quando fu misurato il raggio di Vega, gli astronomi lo trovarono maggiore circa del 50% rispetto al valore atteso per una stella di quella massa e classe spettrale. Nel 2005, grazie all’interferometro CHARA, si capì che ciò era dovuto (Figura 4) alla rapida rotazione di Vega e al fatto che essa rivolge verso di noi il suo polo, quindi noi la osserviamo più “larga” del 23% circa! Non solo, ma se ruotasse più rapidamente anche solo del 9%, la stella stessa si disgregherebbe per effetto della sua stessa rotazione!
Volete esempi più estremi? Achernar (a Eridani) è un’altra stella giovane e dedita alle piroette: 10 volte più grande del Sole, ruota in soli 2 giorni, e sopporta uno schiacciamento polare del 41% senza andare in mille pezzi…! E non dimentichiamo le stelle di neutroni, relitti stellari di poche decine di km ma pesanti alcune volte il nostro Sole, alcune delle quali girano su sé stesse in pochi millisecondi … (leggi l’astrocuriosita` di aprile 2021: “La carica dei quattrocento”)! Ad esempio, la pulsar PSR J1748-2446ad, la più rapida che si conosca, ha un periodo di rotazione di 1.4 ms. Si capisce che, per controbilanciare la forza centrifuga, la loro gravità deve essere immensa ed è proprio così che è possibile mettere dei limiti alla loro massa e al loro raggio, pur essendo oggetti così piccoli da non potersi risolvere nei loro dettagli, nemmeno col più potente dei telescopi. E che dire allora dei buchi neri rotanti, persino la cui ergosfera è schiacciata ai poli…?
Ma torniamo al Sistema Solare: quando nel 2004 fu scoperto il pianeta nano Haumea, che orbita oltre Nettuno, gli astronomi rimasero sorpresi dalla sua forma insolitamente schiacciata; il suo diametro massimo era di 2322 km e quello minimo di 1138 km. Si comprese poco dopo che ciò era dovuto al suo breve periodo di rotazione, di sole 4 ore! Anche altri asteroidi, come Ryugu (Figura 5), presentano marcate distorsioni centrifughe. Non esistono quindi pianeti piatti, ma si potrebbe dire che alcuni pianeti nani si mettano d’impegno per diventarli…!
E torniamo, infine, alla nostra Terra. È abbastanza facile calcolare che all’epoca della formazione della Luna, la Terra faceva un giro sul suo asse in sole 5 ore e mezza! (la rotazione della Terra ha rallentato fino ai valori attuali grazie alle maree …) Questa Terra primordiale era “piatta”? Non ancora… la nostra formula ci fornisce in tal caso una differenza tra raggio polare ed equatoriale di “soli” 500 km, ma si può calcolare che il minimo periodo di rotazione della Terra potrebbe sopportare senza essere smembrata dalla forza centrifuga è di 1 ora e 25 minuti circa.
Si potrebbe vivere su un mondo “appiattito” da una rotazione così rapida?
Non credo che ci piacerebbe.
A parte la forza centrifuga, in un sistema di riferimento rotante compare un’altra forza, quella di Coriolis, che – tranne all’equatore – devia lateralmente tutti i corpi in movimento su di essa, compresi i venti (Figure 6). Se la Terra girasse, diciamo, in 1 ora e 30 minuti… non solo i cicloni avrebbero una potenza inimmaginabile, ma gli aerei verrebbero spontaneamente deviati di rotta: ad esempio, partendo da Roma verso Nord, dopo 2 ore circa di volo ritorneremmo a Roma da Sud, dopo avere fatto un giro panoramico dell’Adriatico in senso orario. Ogni calcio al pallone verrebbe automaticamente ad effetto, e ogni calcio di rinvio rischierebbe di finire in fallo laterale. Ma perfino il nostro sangue verrebbe spinto contro le pareti delle vene circolando al loro interno: pensate che mal di testa avremmo… no no, meglio vivere su una pianeta quasi perfettamente sferico, e lasciamo la piattezza alla pizza e al piatto in cui la serviamo.






